
题目列表(包括答案和解析)
1.不等式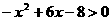 的解集为( )
的解集为( )
A.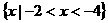 B.
B.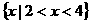 C.
C.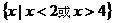 D.
D.
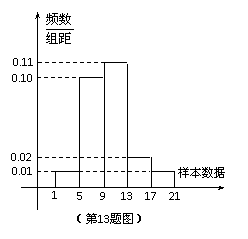 样本数据
样本数据
(13)右图是一个样本容量为 1000 的频率分
布直方图,根据这个图计算,样本中
的数据恰好落在区间 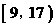 内的概
内的概
率为___________.
(14)若回归直线方程为 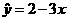 ,
,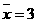 ,
,
则 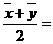 .
.
(15)与向量a 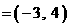 垂直的单位向量为______________________________.
垂直的单位向量为______________________________.
(16)对于函数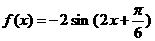 ,下列命题:
,下列命题:
① 图象关于原点成中心对称; ② 图象关于直线 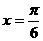 对称;
对称;
③ 图象向左平移 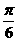 个单位,即得到函数
个单位,即得到函数 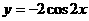 的图象,
的图象,
其中正确命题的序号为 .
三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
|
得 分 |
评 卷 人 |
|
|
|
(17)(本小题满分12分)
(Ⅰ)求 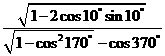 的值;
的值;
(Ⅱ)若 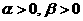 ,且
,且 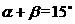 ,求
,求 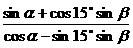 的值.
的值.
(18)(本小题满分12分)
已知函数 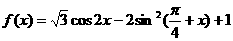 ,
, .
.
(Ⅰ)求 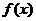 的最大值,并求出当
的最大值,并求出当 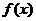 取得最大值时
取得最大值时 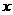 的取值;
的取值;
(Ⅱ)求 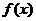 的单调递增区间.
的单调递增区间.
(19)(本小题满分12分)
已知 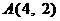 ,
,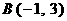 ,
,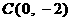 为坐标平面上的三个点,
为坐标平面上的三个点, 为坐标原点,点
为坐标原点,点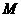 为
为  所在直线上一个动点.
所在直线上一个动点.
(Ⅰ)若 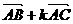 与
与 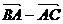 垂直,求
垂直,求 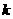 的值;
的值;
(Ⅱ)若向量 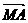 在向量
在向量 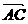 方向上的射影的数量为
方向上的射影的数量为
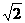 ,求
,求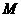 点的坐标.
点的坐标.
(20)(本小题满分12分)
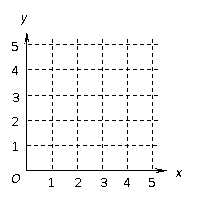 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下表所示:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下表所示:
零件的个数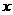 (个) (个) |
2 |
3 |
4 |
5 |
加工的时间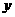 (小时) (小时) |
2.5 |
3 |
4 |
4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;
(Ⅱ)求出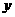 关于
关于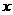 的线性回归方程
的线性回归方程 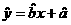 ,
,
并在坐标系中画出回归直线;
(Ⅲ)试预测加工10个零件需要多少时间?
(21)(本小题满分12分)
某学校举办消防知识竞赛,总共 7 个题中,分值为 10 分的有 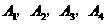 共4 个,分值为 20 分的有
共4 个,分值为 20 分的有 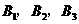 共3个,每位选手都要分别从 4 个 10 分题和 3 个 20 分题中各随机抽取 1 题参赛.已知甲选手 4 个 10 分题中只有
共3个,每位选手都要分别从 4 个 10 分题和 3 个 20 分题中各随机抽取 1 题参赛.已知甲选手 4 个 10 分题中只有  不会,3个 20 分题中只会
不会,3个 20 分题中只会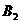 .
.
(Ⅰ)求甲选手恰好得30分的概率;
(Ⅱ)求甲选手得分超过10分的概率.
(22)(本小题满分14分)
已知圆C经过点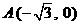 ,圆心落在
,圆心落在 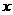 轴上(圆心与坐标原点不重合),且与直线
轴上(圆心与坐标原点不重合),且与直线 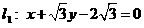 相切.
相切.
(Ⅰ)求圆 C 的标准方程;
(Ⅱ)求直线Y=X 被圆C所截得 的弦长;
(Ⅲ)l2是与l1垂直并且在Y轴上的截距为b的直线,若)l2与圆 C 有两个不同的交点,求b的取值范围.
(1)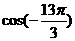 =
=
(A)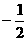 (B)
(B)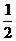 (C)
(C)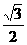 (D)
(D)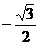
(2)若关于 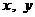 的方程
的方程 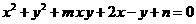 表示的曲线是圆,则
表示的曲线是圆,则 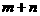 的取值范围是
的取值范围是
(A)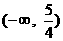 (B)
(B)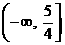 (C)
(C)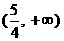 (D)
(D)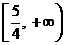
(3)在空间直角坐标系中,点 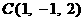 到坐标系原点
到坐标系原点  的距离是
的距离是
(A)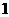 (B)
(B)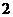 (C)
(C)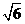 (D)
(D)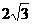
(4)已知扇形的半径为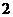 ,面积为
,面积为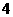 ,则这个扇形圆心角的弧度数为
,则这个扇形圆心角的弧度数为
(A)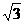 (B)
(B)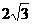 (C)
(C)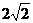 (D)
(D)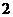
(5)已知向量 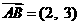 ,
,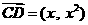 ,若
,若 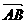 ∥
∥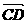 ,则
,则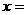
(A)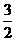 (B)
(B)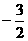 (C)
(C)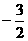 或
或 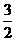 (D)
(D) 或
或 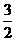
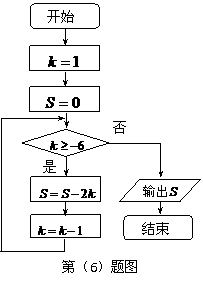 (6)如果执行右面的程序框图,那么输出的
(6)如果执行右面的程序框图,那么输出的 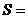
(A)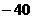 (B)
(B)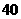
(C) (D)
(D)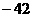
(7)从坐标原点  向圆
向圆 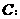
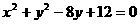
作两条切线,若切点分别为  ,则四边形
,则四边形
 的面积为
的面积为
(A)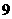 (B)
(B)
(C)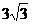 (D)
(D)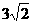
(8)若 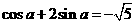 ,则
,则 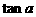 =
=
(A)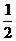 (B)2
(C)
(B)2
(C)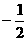 (D)
(D)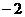
(9)要得到函数 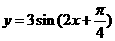 的图像,只需将函数
的图像,只需将函数 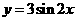 的图像
的图像
(A)向左平移 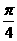 个单位
(B)向右平移
个单位
(B)向右平移 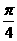 个单位
个单位
(C)向左平移 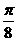 个单位
(D)向右平移
个单位
(D)向右平移 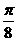 个单位
个单位
(10)已知一个样本的方差为 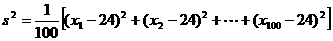 ,若这个样本的容量为
,若这个样本的容量为 ,平均数为
,平均数为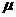 ,则
,则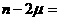
(A) (B)
(B)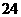 (C)
(C)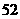 (D)
(D)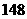
(11)已知函数 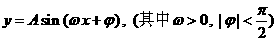 的部分图象如图所示,则这个函数的表达式为
的部分图象如图所示,则这个函数的表达式为
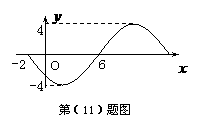 (A)
(A)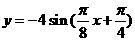
(B)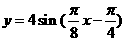
(C)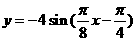
(D)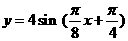
(12)函数 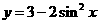 是
是
(A)周期为 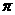 的奇函数
(B)周期为
的奇函数
(B)周期为 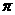 的偶函数
的偶函数
(C)周期为 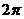 的奇函数
(D)周期为
的奇函数
(D)周期为 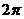 的偶函数
的偶函数
第Ⅱ卷(非选择题 共90分)
2. 答卷前将密封线内的项目填写清楚.
22、(本小题满分14分)图(1)是一个正方体的表面展开图,MN和PQ是两条对角线,请在图(2)的正方体中将MN、PQ画出来,并就这个正方体解答下列各题。
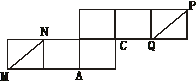
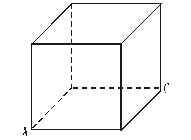
图(1) 图(2)
(1)求MN与PQ所成角的大小。
(2)求四面体M-NPQ的体积与正方体的体积之比。
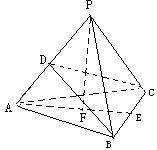
21、(12分)在三棱锥D-ABC中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB。
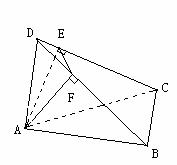 求证:EF⊥DC
求证:EF⊥DC
19.(12分)已知直线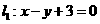 与直线
与直线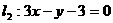 ,
,
求过直线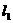 与直线
与直线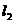 的交点且与直线
的交点且与直线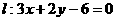 平行的直线方程
平行的直线方程
20(12分)求适合下列条件的直线方程:
(1)经过点P(3,2),且在两坐标轴上的截距相等。
(2)过点A(0,2),且倾斜角的正弦值是0.6。
18、(12分)在三棱锥P-ABC中,AB=PB,AC=PC,AE⊥BC于E,PF⊥AE于F,求证:PF⊥平面ABC
17、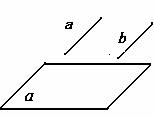 (12分)已知:直线
(12分)已知:直线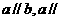 平面
平面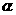 ,
,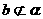 .求证:
.求证: 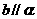
16、已知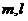 是直线,
是直线, 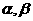 是平面,给出下列命题:
是平面,给出下列命题:
①若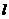 垂直于
垂直于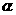 内的两条相交直线,则
内的两条相交直线,则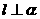 ;
;
②若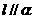 ,则
,则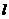 与平面
与平面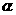 内的所有直线平行;
内的所有直线平行;
③若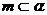 ,
,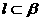 ,且
,且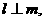 则
则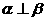 ;
;
④若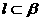 ,且
,且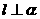 ,则
,则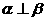 ;
;
⑤若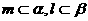 ,且
,且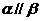 ,则
,则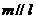 .
.
其中正确命题的序号是
(注:把你认为正确命题的序号都填上)
15.已知直线b//平面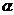 ,平面
,平面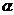 //平面
//平面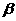 ,则直线b与
,则直线b与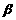 的位置关系为
.
的位置关系为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com