
题目列表(包括答案和解析)
4.设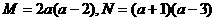 ,则有
( )
,则有
( )

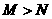
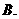
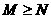

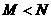
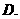
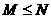
3.已知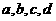 为实数,且
为实数,且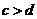 .则“
.则“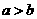 ”是“
”是“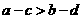 ”的 ( )
”的 ( )
 充分而不必要条件
充分而不必要条件
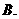 必要而不充分条件
必要而不充分条件
 充要条件
充要条件
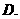 既不充分也不必要条件
既不充分也不必要条件
2. 数列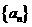 中
中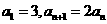 ,则
,则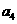 等于
( )
等于
( )

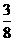
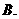
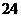

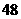
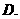
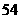
1. 不等式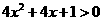 的解集为
( )
的解集为
( )

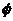
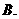
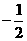


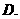
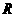
20.(本题满分16分)某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价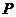 (元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如下表:
|
时间(将第x天记为x)x |
1 |
10 |
11 |
18 |
|
单价(元/件)P |
9 |
0 |
1 |
8 |
而这20天相应的销售量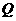 (百件/天)与
(百件/天)与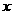 对应的点
对应的点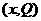 在如图所示的半圆上.
在如图所示的半圆上.
(1)写出每天销售收入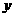 (元)与时间
(元)与时间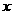 (天)的函数关系式
(天)的函数关系式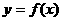 ;
;
 (2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价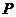 定为多少元为好?(结果精确到1元)
定为多少元为好?(结果精确到1元)
19.(本题满分16分)如图,在平面直角坐标系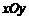 中,
中,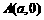
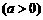 ,
,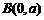 ,
,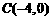 ,
,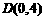 ,设
,设 的外接圆圆心为E.
的外接圆圆心为E.
(1)若⊙E与直线CD相切,求实数a的值;
 (2)设点
(2)设点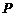 在圆
在圆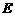 上,使
上,使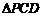 的面积等于12的点
的面积等于12的点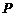 有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
|
18.(本题满分15分)在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=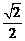 AD,E、F分别是BD、PC的中点.
AD,E、F分别是BD、PC的中点.
 求证:(1)EF//平面PAD; (2)平面PDC⊥平面PAD.
求证:(1)EF//平面PAD; (2)平面PDC⊥平面PAD.
17. (本题满分15分)甲打靶射击,有4发子弹,其中有一发是空弹.
⑴求空弹出现在第一枪的概率;
⑵求空弹出现在前三枪的概率;
⑶如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔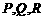 ,第四枪瞄准了三角形
,第四枪瞄准了三角形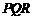 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形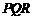 内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
16.(本题满分14分)设锐角三角形ABC的内角A、B、C的对边分别为a、b、c,且满足
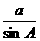 =2b
=2b
(1)求角B的大小;
(2)若a=3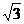 ,c=5,求b的值。
,c=5,求b的值。
15. (本题满分14分)已知直线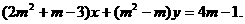
(1)当 为何值时,直线倾斜角为
为何值时,直线倾斜角为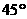 ?
?
(2)当 为何值时,直线与
为何值时,直线与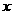 轴平行?
轴平行?
(3)当 为何值时,直线与直线
为何值时,直线与直线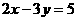 垂直?
垂直?
(4)当 为何值时,直线与直线
为何值时,直线与直线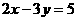 平行?
平行?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com