
题目列表(包括答案和解析)
7.下列四个函数之中,在(0,+∞)上为增函数的是( )
A.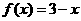 B.
B.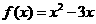 C.
C.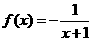 D.
D.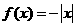
6. 有下列函数:①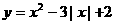 ;②
;②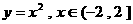 ;③
;③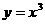 ;④
;④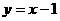 ,其中是偶函数的有:( )
,其中是偶函数的有:( )
A.① B.①③ C.①② D.②④
5. 在下列四组函数中,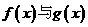 表示同一函数的是 ( )
表示同一函数的是 ( )
A.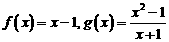 B.
B.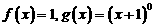
C.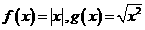 D.
D.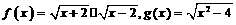
4.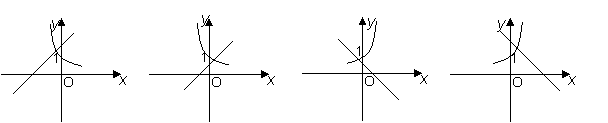 函数
函数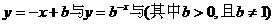 在同一坐标系中的图象只可能是( )
在同一坐标系中的图象只可能是( )
A. B. C. D.
3. 不等式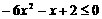 的解集是( )
的解集是( )
A.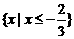 B.
B.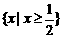 C.
C.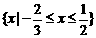 D.
D.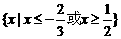
2.若对于任意实数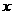 总有
总有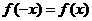 ,且
,且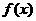 在区间
在区间 上是增函数,则 ( )
上是增函数,则 ( )
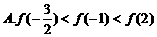
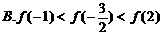
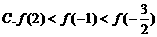
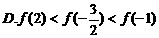
1.若集合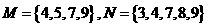 ,全集
,全集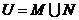 ,则集合
,则集合 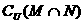 中的元素共有 ( )
中的元素共有 ( )
A. 3个 B . 4个 C . 5个 D . 6个
22.设函数f(x)定义在R上,当x 0时,f(x)
0时,f(x) 1,且对任意a、b
1,且对任意a、b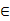 R,都有f(a+b)=f(a)
R,都有f(a+b)=f(a)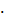 f(b)
f(b)
(1)证明f(0)=1; (2)证明f(x)在R上为增函数;
(3)若f(1)=2,A=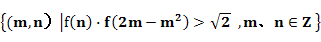 ,
,
B=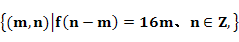 求A
求A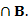
(1)
证明:∵对一切a、b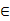 R,都有f(a+b)= f(a)
R,都有f(a+b)= f(a)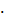 f(b),取a=1,b=0
f(b),取a=1,b=0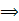 f(1)=f(1)
f(1)=f(1)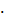 f(0),而x
f(0),而x 0时,f(x)
0时,f(x) 1,∴f(1)
1,∴f(1)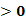 , ∴f(0)=1…………………3分;
, ∴f(0)=1…………………3分;
(2)
证明:先证对一切x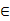 R,都有f(x)
R,都有f(x) 0.
0.
当x 0时,有f(x)
0时,有f(x) 1
1 0;当x=0时,f(x)=1
0;当x=0时,f(x)=1 0;当x
0;当x 0时,f(0)=f(x-x)=f(x)
0时,f(0)=f(x-x)=f(x)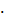 (-x)
(-x)
=f(0)=1 ∴f(x)=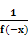 ,而-x
,而-x 0∴f(-x)
0∴f(-x)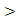 1
1 0,
0, ∴
∴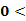 f(x)
f(x) 1.综上对于一切x
1.综上对于一切x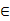 R,都有f(x)
R,都有f(x) 0。
0。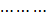 5分;
5分;
任取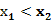 , ∴f(
, ∴f(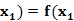 -
-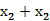 )=f(
)=f(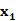 -
-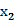 )
)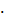 f(
f(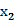 ), ∴
), ∴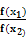 =f(
=f(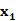 -
-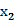 ),
),
∵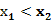 , ∴
, ∴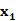 -
-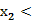 0, ∴
0, ∴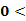 f(
f(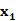 -
-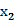 )
) 1,而f(
1,而f(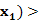 0,f(
0,f(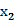 )
) 0,∴f(
0,∴f(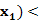 f(
f(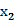 ),故函数f(x)在R上是增函数。
),故函数f(x)在R上是增函数。 8分;
8分;
(3)
解:由f(1)=2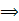 f(
f( +
+ )=
)=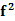 (
(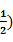 =2
=2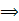 f(
f(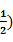 =
=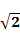 (由(2)知f(x)
(由(2)知f(x) 0),
0),
由f(n)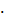 f(2m-
f(2m-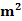 )
)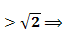 n+2m-
n+2m-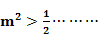 1
1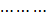 10分;
10分;
由f(4)=f(2)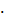 f(2)=
f(2)=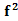 (1)
(1)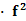 (1)=16=f(n-m),又f(x)在R上是单调函数,∴n-m=4
(1)=16=f(n-m),又f(x)在R上是单调函数,∴n-m=4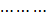 2
2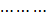 12分;
12分;
由1、2及m、n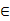 Z解得:m=0,1,2,3,从而求得n=4,5,6,7.
Z解得:m=0,1,2,3,从而求得n=4,5,6,7.
故A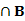 =
=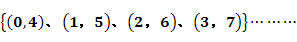 14分
14分
21.已知函数f(x)=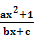 (a、b、c
(a、b、c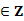 )是奇函数,又f(1)=2,f(2)
)是奇函数,又f(1)=2,f(2)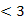 ,且f(x)在[1,+
,且f(x)在[1,+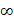 )上递增。(1)求a、b、c的值;(2)当x
)上递增。(1)求a、b、c的值;(2)当x 0时,讨论f(x)的单调区间。
0时,讨论f(x)的单调区间。
解:(1)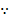 f(-x)=-f(x),又f(-x)=
f(-x)=-f(x),又f(-x)=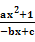 ,∴
,∴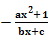 =
=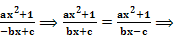 c=0
c=0
∴f(x)=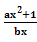
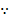 f(1)=2
f(1)=2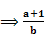 =2
=2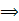 2b=a+1,而f(2)
2b=a+1,而f(2)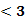 ,f(1)=2,且f(x)在[1,+
,f(1)=2,且f(x)在[1,+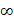 )上是增函数,∴2
)上是增函数,∴2 f(2)
f(2) 3
3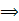 2
2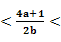 3,将2b=a+1带入得2
3,将2b=a+1带入得2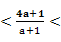 3
3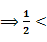 a
a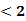 ,而a
,而a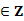 ∴a=1, ∴b=1.综上:a=b=1,c=0………………………6分。
∴a=1, ∴b=1.综上:a=b=1,c=0………………………6分。
(2)由(1)知f(x)=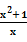 =x+
=x+ .设
.设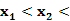 0,则f(
0,则f(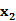 )-f(
)-f(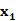 )=(
)=( )(1-
)(1-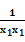 ),
),
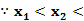 0 ∴
0 ∴ 0,
0,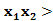 0,当
0,当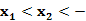 1时,
1时,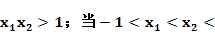 0时
0时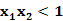 .即当
.即当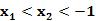 时,f(
时,f(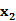 )
) f(
f(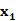 );
);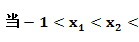 0时f(
0时f(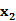 )
) f(
f(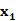 )。故f(x)在(-
)。故f(x)在(-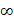 ,-1]上递增,在(-1,0)上递减。……………12分。
,-1]上递增,在(-1,0)上递减。……………12分。
20.集合A=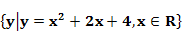 ,B=
,B=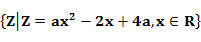 ,若A
,若A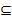 B.求实数a的取值范围。
B.求实数a的取值范围。
解:在A中:y=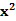 +2x+4=
+2x+4=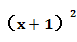 +3
+3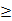 3,
3, A=[3,+
A=[3,+ …………2分.
…………2分.
在B中:z=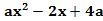 ,
,
1当a=0时,z=-2x,此时z可取一切实数。B=R.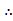 A
A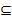 B成立………5分
B成立………5分
2当a 0时,z=a
0时,z=a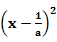 +4a-
+4a- a-
a- ,
,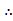 B=(-
B=(-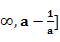 与A
与A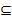 B不符………8分
B不符………8分
3当a 0时,z=a
0时,z=a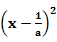 +4a-
+4a-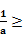 a-
a- ,
,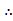 B=
B=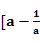 ,+
,+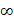 ),由A
),由A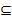 B有
B有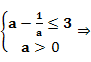 0
0 a
a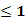 ……………………11分.综上,实数a的取值范围是
……………………11分.综上,实数a的取值范围是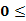 a
a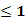 …………12分。
…………12分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com