
题目列表(包括答案和解析)
8.在R上定义运算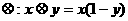 ,若不等式
,若不等式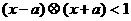 ,对于任意实数x成立,则 ( )
,对于任意实数x成立,则 ( )
A.-1<a<1 B.0<a<2
C.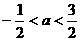 D.
D.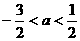
7.若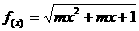 的定义域为R,则m的取值范围 ( )
的定义域为R,则m的取值范围 ( )
A.(0,4) B.[0,4] C.[4, ] D.(0,4 )
] D.(0,4 )
6.若a>b>c则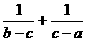 的值是 ( )
的值是 ( )
A.正数 B.负数 C.非正数 D.非负数
5.设a , a+1 , a+2 为纯角三角形的三边,求a的取值范围 ( )
A.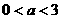 B.
B.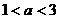 C.
C.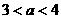 D.
D.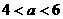
4.某人向东方向走x米,向右转 ,然后朝新方向走3千米,结果离出发点恰好
,然后朝新方向走3千米,结果离出发点恰好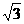 千米,则x的值 ( )
千米,则x的值 ( )
A.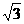 B.2
B.2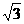 C.2
C.2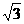 或
或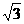 D.3
D.3
3.等腰三角形周长是底边长的5倍,那么顶角余弦值为 ( )
A.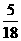 B.
B.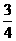 C.
C.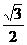 D.
D.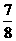
2.在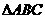 中,B=
中,B=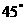 ,C=
,C=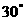 ,c=7,则最短边边长等于 ( )
,c=7,则最短边边长等于 ( )
A.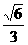 B.
B.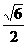 C.
C.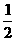 D.
D.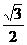
1.在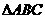 中,sinA=sinC,则
中,sinA=sinC,则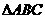 是 ( )
是 ( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
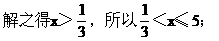
当x>5时,原不等式可化为
x-5-(2x+3)<1,
解之得x>-9,所以x>5.

说明:在含有绝对值的不等式中,“去绝对值”是基本策略.
例13 解不等式|2x-1|>|2x-3|.
分析 本题也可采取前一题的方法:采取用零点分区间讨论去掉绝
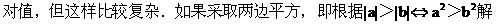
之,则更显得流畅,简捷.
解 原不等式同解于
(2x-1)2>(2x-3)2,
即4x2-4x+1>4x2-12x+9,
即8x>8,得x>1.
所以原不等式的解集为{x|x>1}.
说明:本题中,如果把2x当作数轴上的动坐标,则|2x-1|>|2x-3|表示2x到1的距离大于2x到3的距离,则2x应当在2的右边,从而2x>2即x>1.
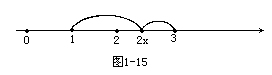
3.本题是一个基础性很强的问题,无论是对立体图形的画法以及空间想象能力的形成都大有裨益.
典型例题十二
例12 下图中表示两个相交平面,其中画法正确的是( ).
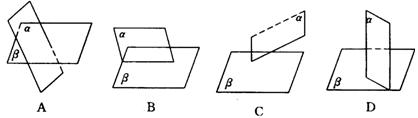
解:对于A,图中没有画出平面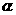 与平面
与平面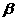 的交线,另外图中的实、虚线也没有按照画法原则去画,因此A的画法不正确.
的交线,另外图中的实、虚线也没有按照画法原则去画,因此A的画法不正确.
同样的道理,也可知B、C图形的画法不正确.
D的图形画法正确.
∴应选D.
说明:对空间图形的准确辨识,是培养空间想象能力的重要组成部分,一定要注意这方面能力的锻炼.
典型例题十三
例13 观察下图,说明图形中的不同之处.

解:上面的图形都是由九条线段构成的图形、外形似乎相似.
仔细观察,由于图中的实、虚线的画法不同,则反映了不同的几何体.
A图是一个簸箕形图形;B图是体,是三棱柱;C图也是体,也是三棱柱.
B图如果看作是从三棱柱的正面观察,C图则可看作是从三棱柱的后面观察.
说明:在立体几何中,一定要明确画图过程中哪条线画实线,哪条线画虚线.要记住:能够看得到的线一定画成实线,被挡住的看不到的线画成虚线.
下面再给出两组图形如下图所示,请同学们予以辨识,指出它们有什么不同.

典型例题十四
例14 若点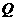 在直线
在直线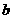 上,
上,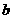 在平面
在平面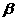 内,则
内,则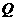 、
、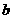 、
、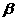 之间的关系可记作( ).
之间的关系可记作( ).
A.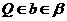 B.
B.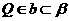 C.
C.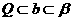 D.
D.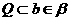
解法1:(直接法)
∵点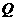 在直线
在直线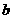 上,∴
上,∴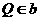 ,
,
∵直线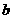 在平面
在平面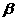 内,∴
内,∴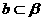 ,
,
∴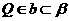 .
.
∴应选B.
解法2:(排除法)
∵点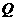 与直线
与直线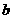 之间的关系是元素与集合之间的关系,
之间的关系是元素与集合之间的关系,
∴只能用符号“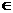 ”或“
”或“ ”表示,
”表示,
∴C、D应予排除.
∵直线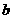 与平面
与平面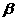 之间是集合与集合之间的关系,
之间是集合与集合之间的关系,
∴只能用符号“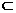 ”或“
”或“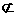 ”表示,
”表示,
∴A应予以排除.
综上可知应选B.
说明:要能正确地使用点、直线、平面之间关系的符号语言.
典型例题十五
例15 用符号语言表示下列语句
(1)点 在平面
在平面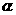 内,但在平面
内,但在平面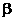 外;
外;
(2)直线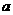 经过平面
经过平面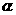 外一点
外一点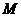 ;
;
(3)直线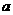 在平面
在平面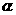 内,又在平面
内,又在平面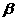 内,即平面
内,即平面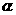 和
和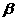 相交于直线
相交于直线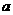 .
.
解:(1) 但
但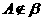 .
.
(2)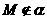 ,
,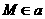 .
.
(3)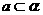 且
且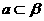 ,即
,即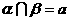 .
.
说明:符号语言比较简洁、严谨,可大大的缩短文字语言表达的长度,有利于推理、计算.
典型例题十六
例16 将下面用符号语言表示的关系改用文字语言予以叙述,并用用图形语言予以表示.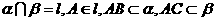 .
.
分析:本题实质是数学三种语言--符号语言、文字语言、图形语言的互译.
解:文字语言叙述为:
点 在平面
在平面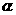 与平面
与平面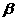 的交线
的交线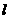 上,
上,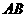 、
、 分别在
分别在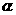 、
、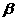 内.
内.
图形语言表示为如图:

说明:文字语言比较自然、生动,它能将问题所研究的对象的含义更加明白地叙述出来,我们教科书上的概念、定理等多以文字语言叙述.
图形语言,易引起清晰的视觉形象,它能直观地表达概念、定理的本质以及相互关系,在抽象的数学思维面前起着具体化和加深理解的作用.
各种数学语言间的互译可为我们在更广阔的思维领域里寻找问题解决的途径提供方便.有利于培养我们思维的广阔性.
典型例题十七
例17 如下图中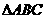 ,若
,若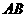 、
、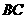 在平面
在平面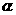 内,判断
内,判断 是否在平面
是否在平面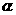 内.
内.

解:∵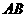 在平面
在平面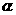 内,
内,
∴ 点一定在平面
点一定在平面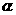 内.
内.
∵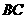 在平面
在平面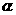 内,
内,
∴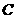 点一定在平面
点一定在平面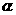 内.
内.
∴点 、点
、点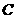 都在平面
都在平面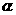 内.
内.
∴直线 在平面内(公理1).
在平面内(公理1).
说明:公理1可以用来判断直线是否在平面内.
典型例题十八
例18 如下图,在正方体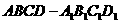 中,
中,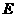 、
、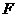 分别为
分别为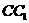 和
和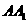 上的中点,画出平面
上的中点,画出平面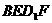 与平面
与平面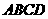 的交线.
的交线.

分析:可根据公理2,如果两个平面有一个公共点,它们就有过这点的一条直线,也只有这一条直线;这条直线的位置还须借助于另一个条件来确定.
解:在平面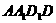 内,延长
内,延长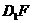 ,
,
∵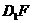 与
与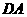 不平行,
不平行,
因此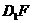 与
与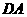 必相交于一点,设为
必相交于一点,设为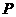
则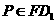 ,
,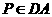 .
.
又∵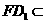 平面
平面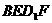 ,
,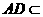 平面
平面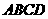 内,
内,
∴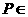 平面
平面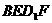 ,
,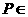 平面
平面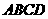 .
.
又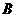 为平面
为平面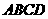 与平面
与平面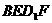 的公共点,
的公共点,
∴连结 ,
, 即为平面
即为平面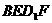 与平面
与平面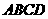 的交线.
的交线.
说明:公理2是两个平面相交的性质,它说明两个平面相交,交线是一条直线.要注意理解两个平面不存在只有一个公共点的情形,如果有一个公共点,那么必定有无数多个公共点,且这些点恰好组成一条直线.同时要注意,找到两个平面的一个公共点,交线的具体位置还无法判定,只有找到两个公共点,才确定这两个平面的交线.这是做几何体截面时确定交线经常用到的方法.
典型例题十九
例19 已知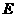 、
、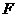 、
、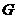 、
、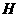 分别是空间四边形
分别是空间四边形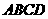 (四条线段首尾相接,且连接点不在同一平面内.所组成的空间图形叫空间四边形.)各边
(四条线段首尾相接,且连接点不在同一平面内.所组成的空间图形叫空间四边形.)各边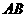 、
、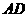 、
、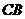 、
、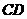 上的点,且直线
上的点,且直线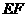 和
和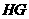 交于点
交于点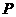 ,如下图,求证:点
,如下图,求证:点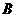 、
、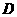 、
、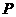 在同一条直线上.
在同一条直线上.
证明:如图

∵直线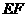
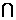 直线
直线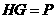 ,
,
∴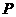
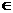 直线
直线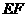 ,而
,而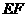
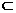 平面
平面 ,
,
∴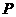
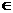 平面
平面 .
.
同理,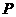
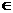 平面
平面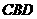 ,即点
,即点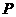 是平面
是平面 和平面
和平面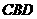 的公共点.显然,点
的公共点.显然,点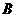 、
、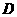 也是平面
也是平面 和平面
和平面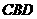 的公共点,由公理2知,点
的公共点,由公理2知,点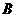 、
、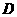 、
、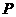 都在平面
都在平面 和平面
和平面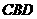 的交线上,即点
的交线上,即点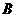 、
、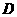 、
、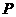 在同一条直线上.
在同一条直线上.
说明:证明三点共线通常采用如下方法:
方法1是首先找出两个平面,然后证明这三点都是这两个平面的公共点,根据公理2知,这些点都在交线上.
方法2是选择其中两点确定一条直线,然后证明另一点在其上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com