
题目列表(包括答案和解析)
3、垂直于同一条直线的两条直线一定
A、平行 B、相交 C、异面 D、以上都有可能
2、下列说法正确的是
A、三点确定一个平面 B、四边形一定是平面图形
C、梯形一定是平面图形 D、平面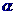 和平面
和平面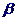 有不同在一条直线上的三个交点
有不同在一条直线上的三个交点
1、线段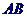 在平面
在平面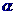 内,则直线
内,则直线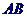 与平面
与平面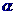 的位置关系是
的位置关系是
A、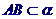 B、
B、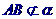 C、由线段
C、由线段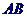 的长短而定 D、以上都不对
的长短而定 D、以上都不对
1.2 正弦定理、余弦定理的应用
 例1(09辽宁理)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
例1(09辽宁理)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为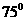 ,
,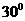 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,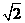
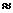 1.414).
1.414).
 变式1-1(09海南文)如图,为了解某海域海底构造,在海平面内一条直线上的
变式1-1(09海南文)如图,为了解某海域海底构造,在海平面内一条直线上的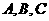 三点进行测量,已知
三点进行测量,已知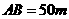 ,
, 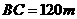 ,于
,于 处测得水深
处测得水深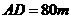 ,于
,于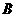 处测得水深
处测得水深 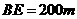 ,于
,于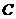 处测得水深
处测得水深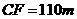 ,求
,求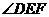 的余弦值.
的余弦值.
例2有一长为1公里的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要伸长( )
A. 1公里 B. sin10°公里 C. cos10°公里 D. cos20°公里
变式2-1在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( )
A.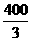 米? B.
米? B.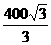 米 C.
米 C.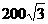 米? D. 200米
米? D. 200米
变式2-2某人站在山顶向下看一列车队向山脚驶来,他看见第一辆车与第二辆车的俯角差等于他看见第二辆车与第三辆车的俯角差,则第一辆车与第二辆车的距离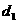 与第二辆车与第三辆车的距离
与第二辆车与第三辆车的距离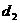 之间的关系为( )
之间的关系为( )
A.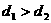 B.
B. 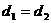 C.
C. 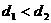 D.不能确定大小
D.不能确定大小
变式2-3为了测量上海东方明珠的高度,某人站在 处测得塔尖的仰角为
处测得塔尖的仰角为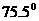 ,前进38.5m后,到达
,前进38.5m后,到达 处测得塔尖的仰角为
处测得塔尖的仰角为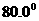 .试计算东方明珠塔的高度(精确到1m).
.试计算东方明珠塔的高度(精确到1m).
1.1 正弦定理、余弦定理
例1在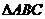 中,已知
中,已知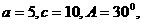 则
则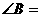 ( )
( )
A.105° B.60° C.15° D.105°或15°
变式1-1在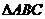 中,若
中,若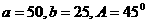 则
则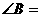 .
.
变式1-2(06江苏)在△ABC中,已知BC=12,A=60°,B=45°,则AC= .
变式1-3在等腰三角形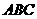 中,已知
中,已知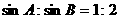 ,底边
,底边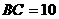 ,则
,则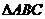 的周长是
.
的周长是
.
例2在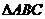 中,已知三边
中,已知三边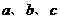 满足
满足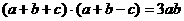 , 则
, 则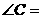 ( )
( )
A.15° B.30° C.45° D.60°
变式2-1若平行四边形两条邻边的长度分别是4cm和4cm,它们的夹角是45°,则这个平行四边形的两条对角线的长度分别为 .
变式2-2(06山东)在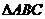 中,角A、B、C的对边分别为a、b、c, A=
中,角A、B、C的对边分别为a、b、c, A=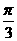 ,a=
,a=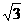 ,b=1,则c
= (
)
,b=1,则c
= (
)
A.1
B.2
C.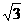 -1
D.
-1
D.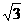
变式2-3边长为5、7、8的三角形的最大角与最小角之和为( )
A.90° B.120° C.135° D.150°
例3在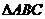 中,若
中,若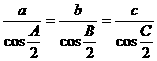 ,则
,则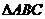 的形状是( )
的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
变式3-1在△ABC中,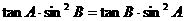 ,那么
,那么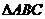 的形状是( )
的形状是( )
A.锐角三角形 B.直角三角形 C.等腰三角形 D.等腰三角形或直角三角形
变式3-2在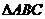 中,
中, 为锐角,
为锐角,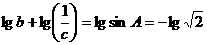 ,则
,则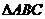 的形状是( )
的形状是( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形
例4在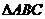 中,若
中,若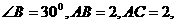 则
则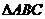 的面积是
.
的面积是
.
变式4-1(06上海)在△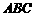 中,已知
中,已知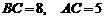 ,三角形面积为12,则
,三角形面积为12,则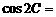 .
.
变式4-2在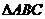 中,
中,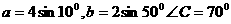 ,则
,则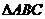 的面积为( )
的面积为( )
A.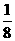 B.
B.
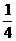 C.
C. 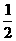 D.
D.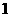
例5(06天津)在 中,
中,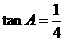 ,
,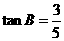 .
.
(Ⅰ)求角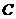 的大小;(Ⅱ)若
的大小;(Ⅱ)若 最大边的边长为
最大边的边长为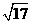 ,求最小边的边长.
,求最小边的边长.
变式5-1(06浙江)已知 的周长为
的周长为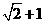 ,且
,且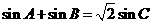 .
.
(I)求边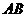 的长;(II)若
的长;(II)若 的面积为
的面积为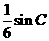 ,求角
,求角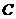 的度数.
的度数.
变式5-2(06全国Ⅰ)设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,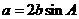 .
.
(Ⅰ)求B的大小;(Ⅱ)若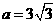 ,
,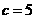 ,求b.
,求b.
6(06山东)在 中,角
中,角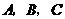 的对边分别为
的对边分别为 .
.
(1)求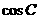 ;(2)若
;(2)若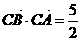 ,且
,且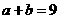 ,求
,求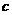 .
.
变式6-1(09浙江理)在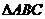 中,角
中,角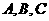 所对的边分别为
所对的边分别为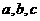 ,且满
,且满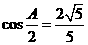 ,
,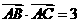 .
.
(Ⅰ)求 的面积;(Ⅱ)若
的面积;(Ⅱ)若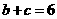 ,求
,求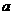 的值.
的值.
变式6-2(09北京理)在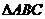 中,角
中,角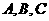 的对边分别为
的对边分别为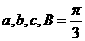 ,
,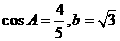 .
.
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求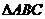 的面积.
的面积.
变式6-3(09安徽理)在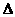 ABC中,
ABC中,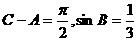 .
.
(Ⅰ)求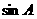 的值;(Ⅱ)设AC=
的值;(Ⅱ)设AC=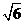 ,求
,求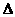 ABC的面积.
ABC的面积.
变式6-4(09江西理)△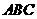 中,
中,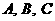 所对的边分别为
所对的边分别为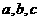 ,
,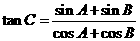 ,
,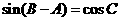 .
.
(Ⅰ)求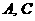 ;(Ⅱ)若
;(Ⅱ)若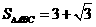 ,求
,求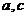 .
.
22.已知集合A={x|x2-3x+2=0},B={x|x2-ax+3a-5},若A∩B=B,求实数a的值.
21.已知集合A=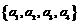 ,B=
,B=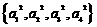 ,其中
,其中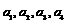 均为正整数,且
均为正整数,且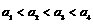 ,A∩B={a1,a4},
a1+a4=10, A∪B的所有元素之和为124,求集合A和B.
,A∩B={a1,a4},
a1+a4=10, A∪B的所有元素之和为124,求集合A和B.
20.设集合A=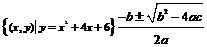 ,B=
,B=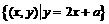 ,问:
,问:
(1) a为何值时,集合A∩B有两个元素;
(2) a为何值时,集合A∩B至多有一个元素.
19.设集合A={x|2x2+3px+2=0};B={x|2x2+x+q=0},其中p,q,x∈R,当A∩B=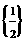 时,求p的值
时,求p的值
和A∪B.
18.设全集U=R,集合A=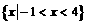 ,B=
,B=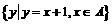 ,试求CUB, A∪B, A∩B,A∩(CUB),
( CU A) ∩(CUB).
,试求CUB, A∪B, A∩B,A∩(CUB),
( CU A) ∩(CUB).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com