
题目列表(包括答案和解析)
3.解:∵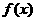 是偶函数,
是偶函数, 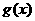 是奇函数,∴
是奇函数,∴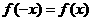 ,且
,且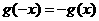
而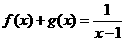 ,得
,得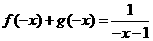 ,
,
即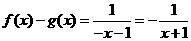 ,
,
∴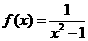 ,
,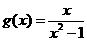 。
。
2.证明:(1)设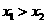 ,则
,则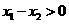 ,而
,而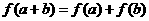
∴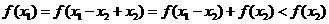
∴函数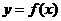 是
是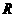 上的减函数;
上的减函数;
(2)由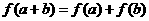 得
得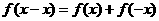
即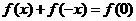 ,而
,而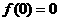
∴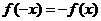 ,即函数
,即函数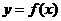 是奇函数。
是奇函数。
1.解:(1)定义域为 ,则
,则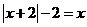 ,
,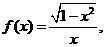
∵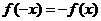 ∴
∴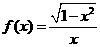 为奇函数。
为奇函数。
(2)∵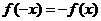 且
且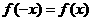 ∴
∴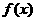 既是奇函数又是偶函数。
既是奇函数又是偶函数。
5. 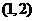
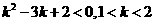
4. 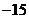
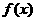 在区间
在区间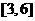 上也为递增函数,即
上也为递增函数,即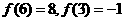
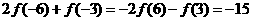
3.
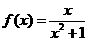
∵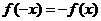 ∴
∴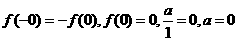
即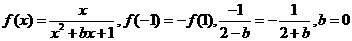
2.
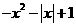 设
设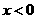 ,则
,则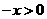 ,
,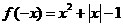 ,
,
∵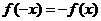 ∴
∴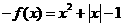 ,
,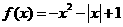
1. 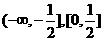 画出图象
画出图象
6. B 刚刚开始时,离学校最远,取最大值,先跑步,图象下降得快!
1. A (1)反例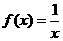 ;(2)不一定
;(2)不一定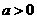 ,开口向下也可;(3)画出图象
,开口向下也可;(3)画出图象
可知,递增区间有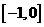 和
和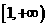 ;(4)对应法则不同
;(4)对应法则不同
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com