
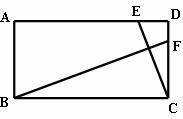
27.(14分)如图,已知在矩形ABCD中,AD=8cm,CD=4cm,点E从点D出发,沿线段DA以每秒1cm的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2cm的速度移动,当B、E、F三点共线时,两点同时停止运动.设点E移动的时间为t(秒),
(1)求证:△BCF∽△CDE;
(2)求t的取值范围;
(3)连结BE,当t为何值时,∠BEC=∠BFC?
26.
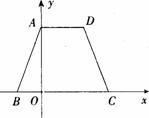
(14分)已知:如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A(
0, 6 ),D
(
4,6),且AB=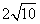 .
.
⑴求点B的坐标;
⑵求经过A、B、D三点的抛物线的解析式;
⑶在⑵中所求的抛物线上是否存在一点P,使得S△PBC = S梯形ABCD?若存在,请求出该点坐标,若不存在,请说明理由.
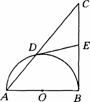
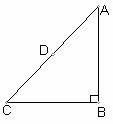
25. (12分)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE.
(1) DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;
(2) 若AD、AB的长是方程x2-10x+24=0的两个根,求直角边BC的长。
24.(10分)如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮。两船同时起航,并同时到达折线A-B-C的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E点( )。
A、在线段AB上 B、在线段BC上 C、可以在线段AB上,也可以在线段BC上
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
23. (10分)我国东南沿海某地的风力资源丰富,一年内日平均风速不小于3米/秒的时间共约160天,其中日平均风速不小于6米/秒的时间约占60天。
为了充分利用“风能”这种“绿色能源”,该地拟建一个小型风力发电场,决定选用A、B两种型号的风力发电机。根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:
日平均风速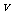 (米/秒) (米/秒) |
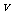 <3 <3 |
3≤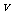 <6 <6 |
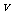 ≥6 ≥6 |
|
|
日发电量(千瓦·时) |
A型发电机 |
0 |
≥36 |
≥150 |
|
B型发电机 |
0 |
≥24 |
≥90 |
根据上面的数据回答:
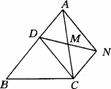
(1)若这个发电场购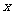 台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦·时;
台A型风力发电机,则预计这些A型风力发电机一年的发电总量至少为_____________千瓦·时;
(2)已知A型风力发电机每台0.3万元,B型风力发电机每台0.2万元,该发电机拟购置风力发电机共10台,希望购机的费用不超过2.6万元,而建成的风力发电场每年的发电总量不少于102000千瓦·时,请你提供符合条件的购机方案。
22、(8分)已知:如图,D是△ABC的边AB上一点,M是AC边的中点,过A作AN∥CD交DM延长线于N,求证:AD=CN.
21、(每小题8分,共16分)
⑴先化简,再求值: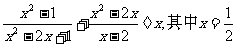
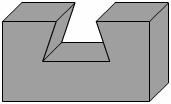
⑵画出下面实物的三视图:
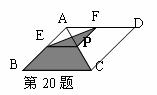
20. 如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是_______.
19、若圆的一条弦长为6 cm,其弦心距等于4 cm,则该圆的半径等于_____ cm.
18、若反比例函数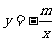 的图象经过点
的图象经过点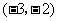 ,则
,则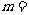 __________.
__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com