1．－2的相反数是(　　 )．

　A．2　　　　　　　 B．一2　　　　　　 C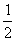．　　　　　　　　 D．一

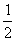
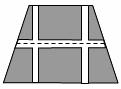
26．如下图，要设计一个等腰梯形的花坛，花坛上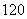底长米，下底长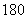米，上下底相距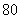米，在两腰中点连线(虚线)处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为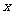米．

(1)用含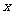的式子表示横向甬道的面积；

(2)当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；

(3)根据设计的要求，甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系，比例系数是5.7，花坛其余部分的绿化费用为每平方米0.02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？

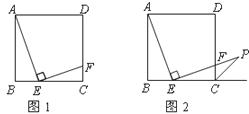
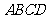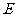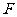25．如图1，在边长为5的正方形中，点、分别是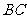、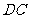边上的点，且，.

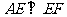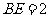(1)求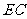∶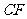的值；

(2)延长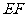交正方形外角平分线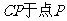(如图13-2)，试判断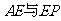的大小关系，并说明理由；

(3)在图2的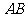边上是否存在一点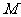，使得四边形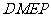是平行四边形？若存在，请给予证明；若不存在，请说明理由．

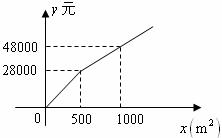
24．南宁市狮山公园计划在健身区铺设广场砖．现有甲、乙两个工程队参加竞标，甲工程队铺设广场砖的造价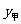(元)与铺设面积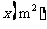的函数关系如下图所示；乙工程队铺设广场砖的造价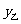(元)与铺设面积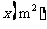满足函数关系式：．

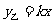(1)根据下图写出甲工程队铺设广场砖的造价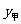(元)与铺设面积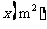的函数关系式；

(2)如果狮山公园铺设广场砖的面积为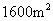，那么公园应选择哪个工程队施工更合算？

23．如下图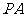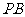，、是半径为1的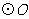的两条切线，点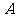、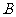分别为切点，

．

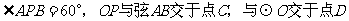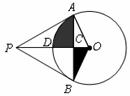
(1)在不添加任何辅助线的情况下，写出图中所有的全等三角形；

(2)求阴影部分的面积(结果保留)．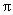

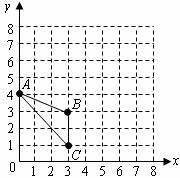
22．已知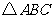在平面直角坐标系中的位置如下图所示．

(1)分别写出图中点的坐标；

(2)画出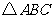绕点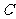按顺时针方向旋转；

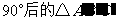(3)求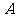点旋转到点所经过的路线长(结果保留)．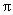

21．为迎接国庆60周年，某校举行以“祖国成长我成长”为主题的图片制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：

请根据以上图表提供的信息，解答下列问题：

(1)表中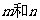所表示的数分别为：；

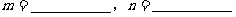(2)请在下图中，补全频数分布直方图；

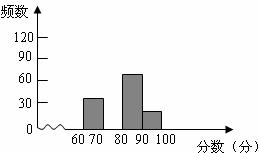
(3)比赛成绩的中位数落在哪个分数段？

(4)如果比赛成绩80分以上(含80分)可以获得奖励，那么获奖率是多少？

20．先化简，再求值：

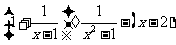，其中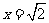

19．计算：

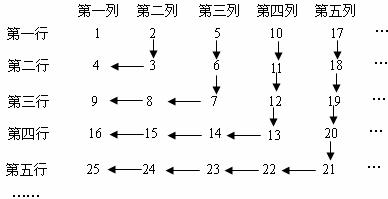
18．正整数按下图的规律排列．请写出第20行，第21列的数字　　　　　 ．