
4、在平面直角坐标系中有两个点A.B,若以点A为坐标原点,则点B的坐标是(3, 4),若以点B为坐标原点,则点A的坐标是( )
A.(–3,–4) B.(–3,4) C.(3,–4) D.(3,4)
3、如图,小明从A处出发沿北偏东600方向行走至B处,又沿北偏西200方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
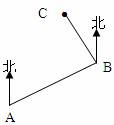
A.左转800 B.右转800 C.左转1000 D.右转1000
2、如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
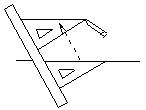
A.两直线平行,同位角相等。 B.内错角相等,两直线平行。
C.同旁内角互补,两直线平行。D.同位角相等,两直线平行。
1、下面四个图形中,∠1与∠2是对顶角的图形 ( )
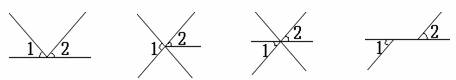
A.1个 B.2个 C.3个 D.4个
26.(本小题满分12分)
如图,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动。伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E。点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止。设点P、Q运动的时间是t秒(t>0).
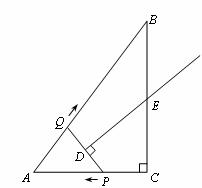
(1)当t = 2时,AP = ,点Q到AC的距离是 ;
(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C 时,请直接写出t的值.
25.(本小题满分12分)
某公司装修需用A型板材240块、B型板材180块,A型板材规格是60 cm×30 cm,B型板材规格是40 cm×30 cm.现只能购得规格是150 cm×30 cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(图是裁法一的裁剪示意图)
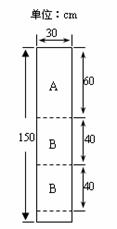
|
|
裁法一 |
裁法二 |
裁法三 |
|
A型板材块数 |
1 |
2 |
0 |
|
B型板材块数 |
2 |
m |
n |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m = ,n = ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式, 并指出当x取何值时Q最小,此时按三种裁法各裁标准板材多少张?
24.(本小题满分10分)
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形。AE的中点是M.
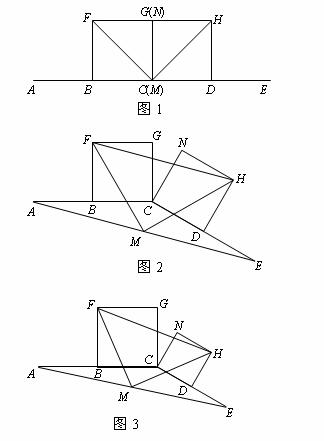
(1)如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,
求证:FM = MH,FM⊥MH;
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图2,
求证:△FMH是等腰直角三角形;
(3)将图2中的CE缩短到图3的情况,△FMH还是等腰直角三角形吗?(不必说明理由)
22.(本小题满分9分)
已知抛物线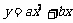 经过点
经过点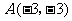 和点P (t,0),且t ≠ 0.
和点P (t,0),且t ≠ 0.
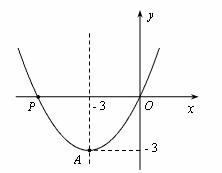
(1)若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值; (2)若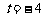 ,求a、b的值,并指出此时抛物线的开口方向;
,求a、b的值,并指出此时抛物线的开口方向;
(3)直接写出使该抛物线开口向下的t的一个值.
21.(本小题满分9分)
某商店在四个月的试销期内,只销售A、B两个品牌的电视机,共售出400台.试销结束后,只能经销其中的一个品牌,为作出决定,经销人员正在绘制两幅统计图,如图1和图2.

图1
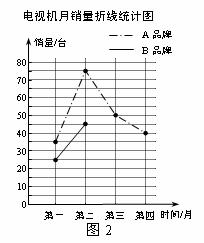
(1)第四个月销量占总销量的百分比是 ;
(2)在图2中补全表示B品牌电视机月销量的折线;
(3)为跟踪调查电视机的使用情况,从该商店第四个月售出的电视机中,随机抽取一台,求抽到B品牌电视机的概率;
(4)经计算,两个品牌电视机月销量的平均水平相同,请你结合折线的走势进行简要分析,判断该商店应经销哪个品牌的电视机.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com