6．在一次中学生田径运动会上，参加男子跳高的14名运动员成绩如下表所示：(　 )

则这些运动员成绩的中位数是

A．1.66　　　　 B．1.67　　　　　 C．1.68　　　　　　 D．1.75

5．一个钢管放在V形架内，下图是其截面图，O为钢管的圆心．如果钢管的半径为25 cm，∠MPN = 60°，则OP =(　 )

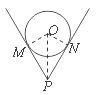
A．50 cm　 　　　　B．25cm　　　 C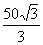．cm　　　　 D．50cm

4．2009年初甲型H1N1流感在墨西哥暴发并在全球蔓延，我们应通过注意个人卫生加强防范．研究表明，甲型H1N1流感球形病毒细胞的直径约为0.00000156 m，用科学记数法表示这个数是(　 )

A．0.156×10^－5　 　　　 B．0.156×10⁵ 　　　　 C．1.56×10^－6 　　　D．1.56×10⁶

3．下图中的正五棱柱的左视图应为(　 )

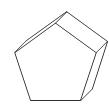
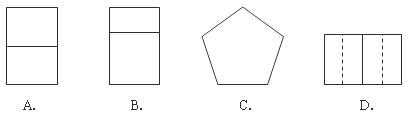
2．点P(－2，1)关于原点对称的点的坐标为(　 )

A．(2，1)　　　 B．(1，－2)　　　 C．(2，－1)　　　 D．(－2，1)

1．如果向东走80 m记为80 m，那么向西走60 m记为(　 )

A．－60 m　　　 B．︱－60︱m　　　 　C．－(－60)m　　 　D．m

23、(本题满分12分)

清朝康熙皇帝是我国历史上一位对数学很感兴趣的帝王。近日，西安发现了他的数学专著，其中有一文《积求勾股法》，他对“三边长为3，4，5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：

“若所设者为积数(面积)，以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数。”

用现在的数学语言表述是：“若直角三角形的三边长分别为3，4，5的整数倍，设其面积为S，则第一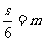步： ；第二步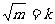：；第三步：分别用3、4、5乘以k，得三边长。”

(1)当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的边长；

(2)你能证明“积求勾股法”的正确性吗？请写出证明过程。

22、(本题满分10分)观察：制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y(℃)，从加热开始计算的时间为x(分钟)．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系(如图)．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．

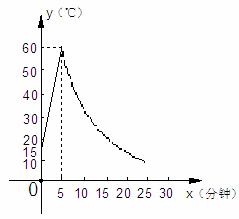
(1)分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；

(2)根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？

21、(本题满分10分)在新农村建设中，我市某乡镇决定对一段公路进行改造，已知这项工程由甲工程队单独做需要40天完成；如果由乙工程队先单独做10天，那么剩下的工程还需要两队合做20天才能完成。

(1)求乙工程队单独完成这项工程所需的天数。

(2)求两队合做完成这项工程所需的天数。

20、(本题满分10分)解方程：

①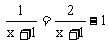的解x=　　　 ．

②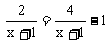的解x=　　　 ．

③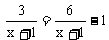的解x= 　　　．

④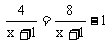的解x=　　　 ．

……

(1)根据你发现的规律直接写出⑤，⑥个方程及它们的解．

(2)请你用一个含正整数n的式子表示上述规律，并求出它的解．