
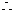 (4-2)+(
(4-2)+( 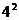 -
-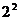 )+…+(
)+…+( 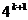 -
-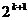 )+
)+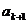 =
=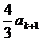 -
-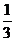

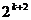 +
+ ,得:
,得: 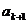 =
=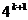 -
-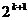 .
.
则当n=k+1时,由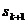 =
=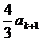 -
-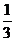

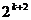 +
+ ,得
,得 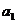 +
+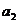 +
+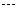
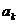 +
+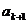 =
=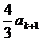 -
-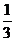

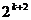 +
+ ,
,
2)假设n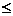 k时成立,即
k时成立,即 =
=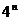 -
- ,n=1,2,
,n=1,2,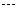 k
k
猜想:  =
=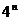 -
- .
.
下用数学归纳法证明:1)当n=1时,显然成立.
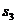 =
=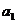 +
+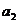 +
+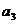 =
=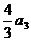 -
-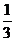

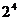 +
+
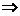
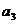 =56=
=56=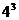 -
-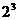 .
.
又由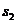 =
=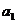 +
+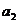 =
=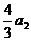 -
-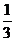

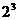 +
+
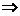
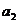 =12=
=12=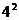 -
-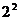 ,
,
由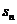 =
=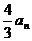 -
-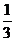

 +
+ , 得:
, 得: 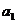 =
=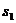 =
=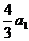 -
-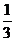
 4+
4+ ,
, 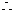
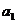 =2.
=2.
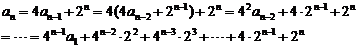
转化为等比数列求和问题.
本题也可利用数学归纳法进行,证明如下:
对于第三种手段,可直接把递推关系 =4
=4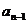 +
+ 直接迭代,即
直接迭代,即
对于前两种手段,求通项公式时,都须对所得递推关系进行变形,转化为等比数列或可求通项的其他数列来解决问题,如(2)中把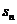 =4
=4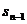 +
+ -2变形为
-2变形为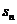 +
+ -
- =4(
=4(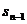 +
+ -
- ),得出数列{
),得出数列{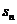 +
+ -
- }为等比数列,进而求出
}为等比数列,进而求出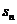 ,然后利用
,然后利用 =
=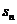 -
-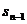 求出
求出 .对于(1)中的递推关系
.对于(1)中的递推关系 =4
=4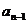 +
+ ,变形的手段更多,如变为
,变形的手段更多,如变为 +
+ =4(
=4(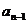 +
+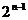 ),n=2,3…,得出数列{
),n=2,3…,得出数列{ +
+ }为等比数列求出
}为等比数列求出 ;也可变形为
;也可变形为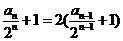 利用等比数列通项公式求解或变形为
利用等比数列通项公式求解或变形为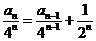 利用叠加的方法求解;还可以通过
利用叠加的方法求解;还可以通过 =4
=4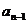 +
+ 及
及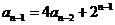 变形为
变形为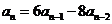 利用特征根思想求解.
利用特征根思想求解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com