
 |
分析:本小题主要考查线面垂直、直线和平面所成的角、二面角等基础知识,以及空间线面位置关系的证明、角和距离的计算等,考查空间想象能力、逻辑推理能力和运算能力.
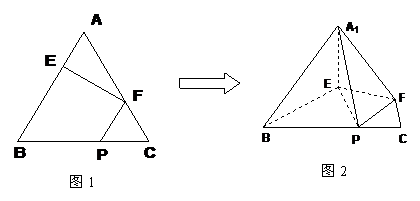
例1(2007江苏卷)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到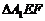 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示).


(二)求空间的角
空间角的计算步骤:一作、二证、三算.
(II)若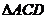 为正三角形,试判断点
为正三角形,试判断点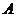 在平面
在平面 内的射影
内的射影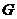 是否在直线
是否在直线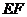 上,证明你的结论,并求角
上,证明你的结论,并求角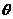 的余弦值.
的余弦值.
(I) 证明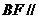 平面
平面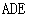 ;
;
例3 例(2007辽宁卷)已知正方形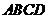 .
.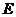 、
、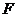 分别是
分别是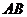 、
、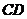 的中点,将
的中点,将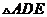 沿
沿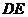 折起,如图所示,记二面角
折起,如图所示,记二面角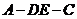 的大小为
的大小为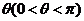 .
.
C.若m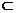
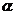 ,n∥
,n∥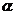 ,则m∥n
D.若m、n与
,则m∥n
D.若m、n与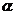 所成的角相等,则n∥m
所成的角相等,则n∥m
分析:本题主要考查直线与平面的平行、垂直的判定.
解析:由直线和平面的位置关系及所成角的有关知识知A、B、D都是错误的,应选C.
点评:熟练掌握线面平行和垂直的有关定理和结论是解决此类问题的关键.
A.若m⊥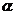 ,m⊥n,则n∥
,m⊥n,则n∥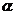 B.若m∥
B.若m∥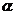 ,n∥
,n∥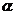 ,则m∥n
,则m∥n
例2 (2007福建卷)对于平面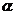 和共面的直线m、n,下列命题中真命题是( )
和共面的直线m、n,下列命题中真命题是( )
④若直线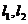 是异面直线,则与
是异面直线,则与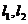 都相交的两条直线是异面直线.
都相交的两条直线是异面直线.
其中假命题的个数是
(A)1 (B)2 (C)3 (D)4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com