1．设集合 =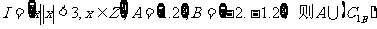

A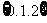． 　　　　　 B．{－2，一1，1，2}

C．{0，1}　　　 　　　 D．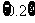

22．(本小题满分12分)

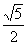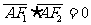　　 已知离心率为的双曲线G的中心在坐标原点，左、右焦点F₁、F₂在x 轴上，双曲线G的右支上一点A使 且△F₁AF₂的面积为l

(I)求双曲线G的标准方程，

(Ⅱ)若直线 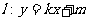与双曲线 G相交于P、Q两点(不重合于左、右顶点)，且以PQ为直径的圆过双曲线G的右顶点D．求证：直线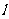过定点'并求出该点的坐标；

21．(本小题满分12分)

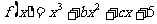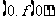　　 已知函数，且曲线 在点 处的切线与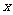 轴平行。

(I)求实数c的值；

(Ⅱ)判断是否存在实数b，使得方程 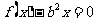　恰有一个实数根．若存在，求b的取值范围；若不存在，请说明理由．

20．(本小题满分12分)

在斜三棱柱ABC-A₁B₁C₁中，已知侧面A₁ACC₁⊥底面ABC底面 ABC是边长为2的正三角形，A₁A=A₁C，A_lA⊥A₁C

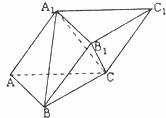
(I)求证：A₁C₁⊥B₁C

(Ⅱ)求二面角B₁-A₁C-C₁的大小

19．(本小题满分12分)

食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测，如果四项指标中的第四项不合格或其它三项指标中有两项不合格，则这种品牌的食品不能上市．已知每项检测是相互独立，第四项指标抽检出现不合格的概率是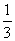，且其它三项指标抽检出现不合格的概率均是．

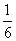(I)若食品监管部门要对其四项质量指标依次进行严格的检测，求恰好在第三硬指标检测结束时，能确定该食品不能上市的概率；

(Ⅱ)求该品牌的食品能上市的概率．

18．(本小题满分12分)

　　 已知数列 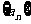满足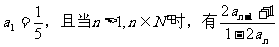

(I)求证：数列 为等差数列；

(Ⅱ)试问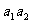是否是数列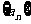 中的项?如果是，是第几项；如果不是，请说明理由

17．(本小题满分10分)

　 已知函数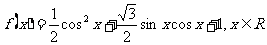

(I)求函数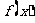，的单调增区间；

(1I)当函数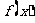，取得最大值时，求自变量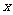的集合．

16．在下列命题中：

　　 ① 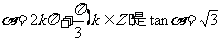的充分不必要条件，

　　 ②函数 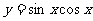的最小正周期是2；

　　 ③在 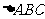中，若cosAcosB>sinAsinB，则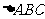为钝角三角形；

　　 ④函数 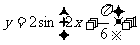图象的对称中心为 。

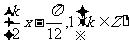　　 其中正确的命题为　　　　　　　 ．(请将正确命题的序号都填上)

15．某校有教师200名，男学生1800名，女学生1600名，现用分层抽样的方法从所有师生中抽出一个容量为n的样本，已知女学生中抽出的人数为80，则n=　　　　　 ．

14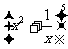．的展开式中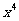的系数是　　　　　 (用数字作答)