
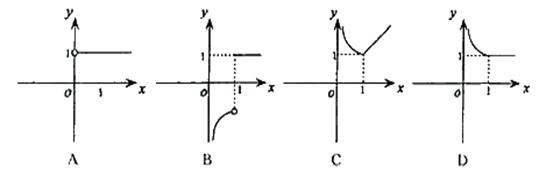
8. 函数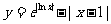 的图象大致是( ).
的图象大致是( ).
7. 已知集合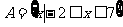 ,
,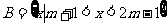 ,且
,且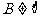 ,若
,若
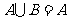 ,则( ).
,则( ).
A.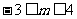 B.
B.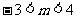 C.
C.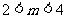 D.
D.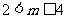
6. 已知向量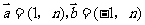 ,若
,若 与
与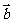 垂直,则
垂直,则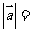 ( ).
( ).
A.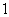 B.
B.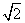 C.
C.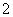 D.4
D.4
5. 已知函数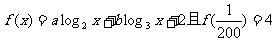 ,则f(200)的值为( ).
,则f(200)的值为( ).
A.-4 B.2 C.0 D.-2
4. 已知函数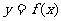 的图象在点
的图象在点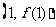 处的切线方程是
处的切线方程是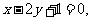
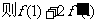 的值是( ).
的值是( ).
A.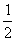 B.1 C.
B.1 C.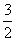 D.2
D.2
3. 若函数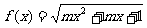 的定义域为R,则m的取值范围是(
).
的定义域为R,则m的取值范围是(
).
A.(0,4) B.[0,4] C.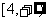 D.
D.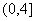
2. 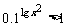 是
是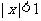 的 ( ).
的 ( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
1. 集合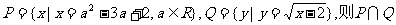 =( ).
=( ).
A.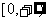 B.
B.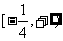 C.
C.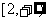 D.
D.
22.(本小题满分14分)
探究函数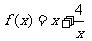 ,
,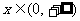 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
(1)请观察表中y值随x值变化的特点,完成以下的问题:
函数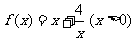 在区间(0,2)上递减;
在区间(0,2)上递减;
函数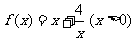 在区间
上递增.
在区间
上递增.
当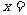 时,
时,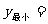 .
.
(2)证明:函数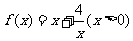 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考:函数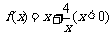 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
21.(本小题满分12分)
已知函数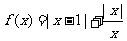
(1)写出去掉绝对值符号后的函数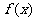 的分段函数解析式;
的分段函数解析式;
(2)画出函数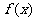 的图象;
的图象;
(3)写出函数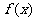 的单调递增区间和单调递减区间.
的单调递增区间和单调递减区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com