
2.设全集U=﹛0,1,2,3,4﹜,集合A={0,1,2,3},B={2,3,4},则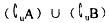 =( )
=( )
A.{0} B{0,1} C.{0,1,4} D.{0,1,2,3,4}
1.如果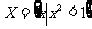 ,那么 ( )
,那么 ( )
A.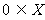 B.
B.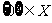 C.
C.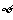
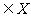 D.
D.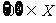
(17)(本小题满分12分)
函数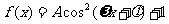
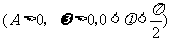 的最大值为3,它的图像相邻的两个对称轴之间的距离为2,图像在
的最大值为3,它的图像相邻的两个对称轴之间的距离为2,图像在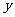 轴上的截距为2。
轴上的截距为2。
(I)求函数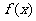 的解析式:
的解析式:
(II)设数列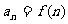
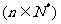 ,
,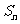 是它的前
是它的前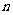 项和,求
项和,求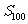 。
。
(18)(本小题满分12分)
已知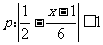 ,
, ,若
,若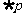 是
是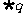 的必要而不充分条件,求实数
的必要而不充分条件,求实数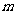 的取值范围。
的取值范围。
(19)(本小题满分12分)
已知△ABC的内角A、B、C的对边分别为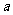 、
、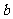 、
、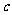 ,向量
,向量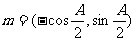 ,
,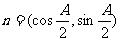 ,且满足
,且满足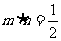 。
。
(I)若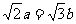 ,求
,求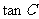 。
。
(II)若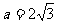 ,△ABC的面积
,△ABC的面积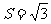 ,求△ABC的周长。
,求△ABC的周长。
(20)(本小题满分12分)
解关于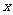 的不等式
的不等式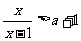
(21)(本小题满分12分)
已知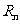 是数列
是数列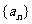 的前
的前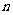 项和,且
项和,且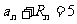 。
。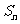 是等差数列
是等差数列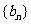 的前
的前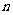 项和,且
项和,且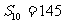 ,
, 。
。
(I)求数列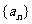 和
和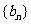 的通项公式;
的通项公式;
(II)设数列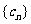 的前
的前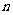 项和为
项和为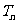 ,且
,且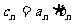 ,求证
,求证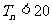 。
。
(22)(本小题满分14分)
已知函数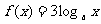 和
和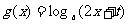
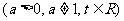 的图像在
的图像在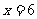 处的切线互相平行。
处的切线互相平行。
(I)求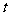 的值;
的值;
(II)设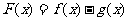 ,且当
,且当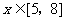 时,
时,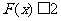 恒成立,求
恒成立,求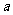 的取值范围。
的取值范围。
(13)下列命题:
①“若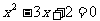 ,则
,则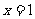 ”的逆否命题为:“若
”的逆否命题为:“若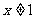 ,则
,则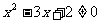 ”;
”;
②“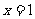 ”是“
”是“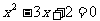 ”的充分不必要条件;
”的充分不必要条件;
③若 为假命题,则
为假命题,则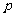 、
、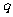 均为假命题;
均为假命题;
④若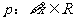 ,使得
,使得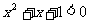 ,则
,则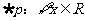 ,均有
,均有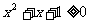 ,
,
其中说法错误的是_________。(将错误命题的序号全部写出来)
(14)函数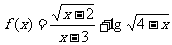 的定义域是_________。
的定义域是_________。
(15)不等式组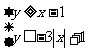 在坐标平面上所表示的平面区域的面积为_________。
在坐标平面上所表示的平面区域的面积为_________。
(16)设函数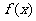 ,
,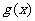 分别是定义在
分别是定义在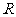 上的奇函数和偶函数,已知当
上的奇函数和偶函数,已知当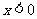 时,有
时,有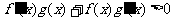 ,且
,且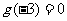 ,则不等式
,则不等式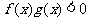 在R上的解集是_________。
在R上的解集是_________。
(1)tan675°的值为
(A)1 (B)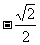 (C)-1 (D)
(C)-1 (D)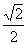
(2)已知实数a∈{-1,1,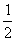 ,2),能使函数
,2),能使函数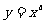 为奇函数且定义域为R的所有
为奇函数且定义域为R的所有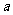 的个数有
的个数有
(A)0个 (B)1个 (C)2个 (D)3个
(3)已知向量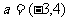 ,则与
,则与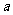 方向相反的单位向量是
方向相反的单位向量是
(A)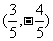 (B)
(B)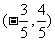 (C)
(C)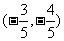 (D)
(D)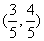
(4)函数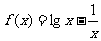 的零点所在的区间是
的零点所在的区间是
(A)(0,1) (B)(1,10) (C)(10,100) (D)(100,+∞)
(5)函数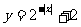 的值域是
的值域是
(A)(0,2) (B)(1,3) (C)(2,3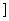 (D)[3,+∞)
(D)[3,+∞)
(6)若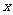 ,
,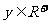 ,且
,且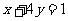 ,则
,则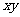 的最大值是
的最大值是
(A)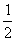 (B)
(B)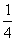 (C)
(C)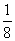 (D)
(D)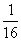
(7)在△ABC中,D是AB边上的一个点,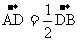 ,
,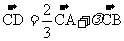 ,则
,则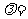
(A)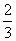 (B)
(B)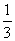 (C)
(C)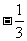 (D)
(D)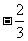
(8)如果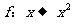 是集合A到B的映射,且B={1,3},则
是集合A到B的映射,且B={1,3},则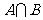 只可能是
只可能是
(A)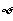 或{1}
(B)(1,3)
或{1}
(B)(1,3)
(C)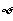 或{3} (D)
或{3} (D)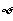 或{1}或{3}
或{1}或{3}
(9)为了得到函数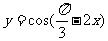 的图像,可以将函数
的图像,可以将函数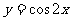 的图像
的图像
(A)向右平移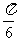 个单位长度 (B)向右平移
个单位长度 (B)向右平移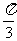 个单位长度
个单位长度
(C)向左平移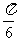 个单位长度 (D)向左平移
个单位长度 (D)向左平移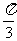 个单位长度
个单位长度
(10)已知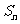 是等比数列{
是等比数列{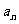 }的前
}的前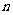 项和,
项和,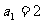 ,数列{
,数列{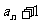 }也是等比数列,
}也是等比数列,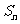 =
=
(A)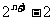 (B)
(B)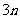 (C)
(C)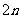 (D)
(D)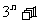
(11)设集合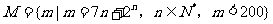 ,则
,则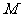 中所有元素的和是
中所有元素的和是
(A)383 (B)450 (C)519 (D)265
(12)函数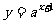 与
与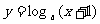 (其中
(其中 且
且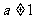 )的图像关于
)的图像关于
(A)直线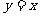 对称 (B)直线
对称 (B)直线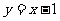 对称
对称
(C)直线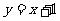 对称 (D)直线
对称 (D)直线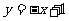 对称
对称
第II卷(非选择题 共90分)
(17)(本小题满分12分)
函数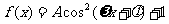
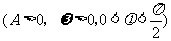 的最大值为3,它的图像相邻的两个对称轴之间的距离为2,图像在
的最大值为3,它的图像相邻的两个对称轴之间的距离为2,图像在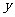 轴上的截距为2。
轴上的截距为2。
(I)求函数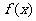 的解析式:
的解析式:
(II)设数列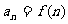
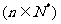 ,
,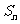 是它的前
是它的前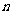 项和,求
项和,求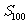 。
。
(18)(本小题满分l2分)
已知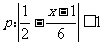 ,
, ,若
,若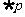 是
是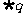 的必要而不充分条件,求实数
的必要而不充分条件,求实数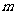 的取值范围。
的取值范围。
(19)(本小题满分12分)
已知△ABC的周长为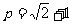 ,且
,且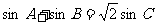 。
。
(I)求边AB的长。
(II)若△ABC的面积为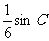 ,求角C的度数。
,求角C的度数。
(20)(本小题满分12分)
解关于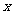 的不等式
的不等式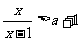
(21)(本小题满分12分)
已知在数列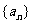 中,
中,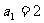 ,
,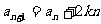 (
(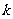 是常数,
是常数,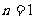 ,2,3,…),且
,2,3,…),且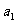 ,
,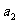 ,
,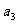 成公比不为1的等比数列。
成公比不为1的等比数列。
(I)求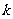 的值;
的值;
(II)求数列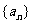 的通项公式。
的通项公式。
(22)(本小题满分14分)
已知函数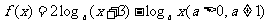
(I)讨论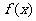 的单调性;
的单调性;
(II)若当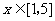 时,
时,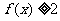 恒成立,求
恒成立,求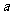 的取值范围。
的取值范围。
(13)下列命题:
①“若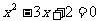 ,则
,则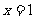 ”的逆否命题为:“若
”的逆否命题为:“若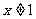 ,则
,则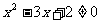 ”;
”;
②“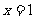 ”是“
”是“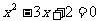 ”的充分不必要条件;
”的充分不必要条件;
③若 为假命题,则
为假命题,则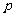 、
、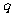 均为假命题;
均为假命题;
④若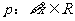 ,使得
,使得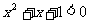 ,则
,则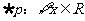 ,均有
,均有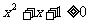 ,
,
其中说法错误的是_________。(将错误命题的序号全部写出来)
(14)函数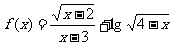 的定义域是_________。
的定义域是_________。
(15)不等式组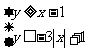 在坐标平面上所表示的平面区域的面积为_________。
在坐标平面上所表示的平面区域的面积为_________。
(16)设函数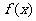 ,
,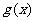 分别是定义在
分别是定义在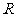 上的奇函数和偶函数,已知当
上的奇函数和偶函数,已知当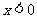 时,有
时,有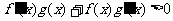 ,且
,且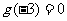 ,则不等式
,则不等式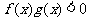 在R上的解集为_________。
在R上的解集为_________。
(1)tan675°的值为
(A)1 (B)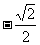 (C)-1 (D)
(C)-1 (D)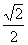
(2)已知实数a∈{-1,1,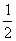 ,2),能使函数
,2),能使函数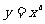 为奇函数且定义域为R的所有
为奇函数且定义域为R的所有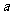 的个数有
的个数有
(A)0个 (B)1个 (C)2个 (D)3个
(3)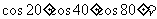
(A)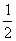 (B)
(B)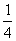 (C)
(C)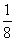 (D)
(D)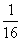
(4)函数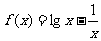 的零点所在的区间是
的零点所在的区间是
(A)(0,1) (B)(1,10) (C)(10,100) (D)(100,+∞)
(5)函数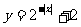 的值域是
的值域是
(A)(0,2) (B)(1,3) (C)(2,3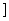 (D)[3,+∞)
(D)[3,+∞)
(6)若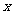 ,
,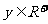 ,且
,且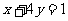 ,则
,则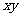 的最大值是
的最大值是
(A)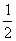 (B)
(B)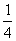 (C)
(C)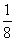 (D)
(D)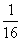
(7)曲线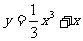 在点(1,
在点(1,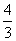 )处的切线与坐标轴围成的三角形面积为
)处的切线与坐标轴围成的三角形面积为
(A)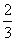 (B)
(B)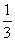 (C)
(C)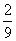 (D)
(D)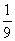
(8)如果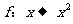 是集合A到B的映射,且B={1,3},则
是集合A到B的映射,且B={1,3},则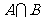 只可能是
只可能是
(A)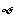 或{1}
(B)(1,3)
或{1}
(B)(1,3)
(C)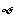 或{3} (D)
或{3} (D)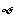 或{1}或{3}
或{1}或{3}
(9)为了得到函数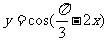 的图像,可以将函数
的图像,可以将函数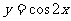 的图像
的图像
(A)向右平移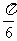 个单位长度 (B)向右平移
个单位长度 (B)向右平移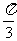 个单位长度
个单位长度
(C)向左平移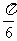 个单位长度 (D)向左平移
个单位长度 (D)向左平移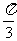 个单位长度
个单位长度
(10)已知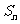 是等比数列{
是等比数列{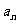 }的前
}的前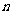 项和,
项和,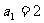 ,数列{
,数列{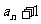 }也是等比数列,
}也是等比数列,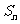 =
=
(A)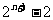 (B)
(B)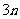 (C)
(C)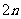 (D)
(D)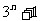
(11)设集合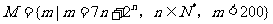 ,则M中所有元素的和是
,则M中所有元素的和是
(A)383 (B)450 (C)519 (D)265
(12)函数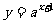 与
与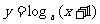 (其中
(其中 且
且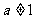 )的图像关于
)的图像关于
(A)直线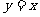 对称 (B)直线
对称 (B)直线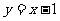 对称
对称
(C)直线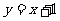 对称 (D)直线
对称 (D)直线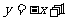 对称
对称
第II卷(非选择题 共90分)
22.已知函数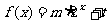 的图象经过点A(1,1),B(2,3)及C(
的图象经过点A(1,1),B(2,3)及C(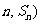 ,
,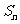 为数列
为数列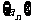 的前
的前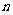 项和.
项和.
(1)求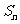 和
和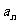 ;
;
(2)若数列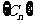 满足
满足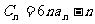 ,求数列
,求数列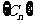 的前
的前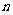 项和
项和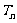 ;
;
(3)比较2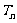 与
与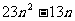 的大小.
的大小.
21.一列火车自上海驶往北京,沿途有n个车站(包括起点上海和终点北京),火车上有一节邮政车厢,每停靠一站便要卸下前面各车站发往该车站的邮袋各一个,同时又要装上该车站发往后面各车站的邮袋各一个,试求:
(1)火车从第k个车站出发时,邮政车厢内共有邮袋数是多少个?
(2)第几个车站的邮袋数最多?最多是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com