22、已知命题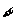：“x∈{x|–1< x <1}，使等式x²–x–m = 0成立”是真命题，

(1)求实数m的取值集合M；

(2)设不等式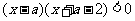的解集为N，若x∈N是x∈M的必要条件，求a的取值范围.

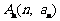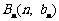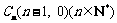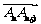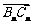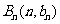附加题在平面直角坐标系中，已知、、，满足向量与向量共线，且点与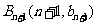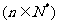都在斜率为6的同一条直线上．(1)若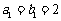，求数列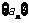的通项公式；

(2)若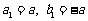，且12＜a≤15，求数列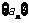中的最小值的项．

21、甲、乙两艘船驶向一个不能同时停泊两艘轮船的码头停泊，它们在一个昼夜内到达的时刻是等可能的，如果甲船停泊的时间是4小时，乙船停泊的时间是6小时，求它们中至少有一艘在停靠泊位时必须等待的概率.

20、对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度(m/s)的数据如下表.

(1)画出茎叶图。

(2)分别填出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、众数、

标准差，并说明选谁参加比赛更合适.

19、求不等式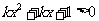的解集为R的

充要条件.　　　　　　　　 .

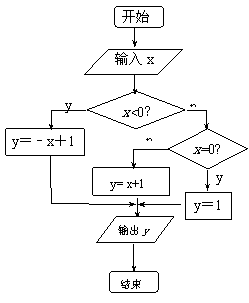
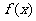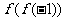18、右边是计算一个函数值的算法框图，设这个函　 数的解析式是y=,试求的值　　　 　　

17、已知命题p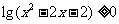：；命题q：0<x<5。若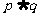为假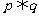，为真，求实数x的取值范围。

B　 卷(满分50分)

16、对某电子元件进行寿命追踪调查，画出频率分布直方图如下.

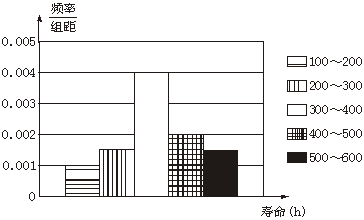
(1)请填写完整样本频率分布表；

(2)估计电子元件寿命在400 h以上的概率.

(3)估计这批电子元件的平均寿命。

15、一只口袋装有形状、大小都相同的白球、红球共8个，其中有2个红球，先由甲然后由乙各摸一颗球，求：(1)甲摸一颗红球的概率；　　

　(2)甲、乙都摸一颗红球的概率；(3)甲或乙摸到红球的概率.　　　　　　　　

14、当X＝5时，右面程序运行的结果是　 　　　　.　　　　　

13、从一个鱼池中捕出n条鱼并标上记号放回池中，一段时间后，再从池中捕出M条鱼，发现其中有记号的鱼有k条，那么可以估计这个鱼池中鱼的条数是　　　　 .