
1.如果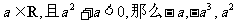 的大小关系是 ( )
的大小关系是 ( )
A.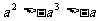 B.
B.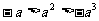
C.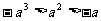 D.
D.
22.(本小题满分14分)
已知函数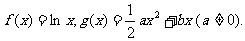
(I)若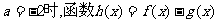 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数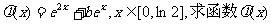 的最小值;
的最小值;
(III)设函数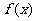 在图象C1与函数
在图象C1与函数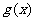 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
21.(本小题满分12分)
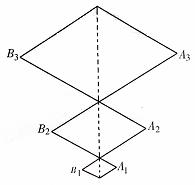
小明同学观察到某建筑物的一墙面上对称排列着一组正三角形架(图示),每个正三角形架的顶点A1、A2、A3、…、A20及B1、B2、B3、…、B20上各有一盏照明灯.已知这些正三角形架的边长依次是10cm,30cm,50cm,…构成一等差数列,这些灯似乎连缀成一条曲线.他断定些灯在同一条抛物线上.
(I)证明他的判断,并求出抛物线的方程;
(II)已知直线l与抛物线的对称轴所在直线垂直,抛物线的顶点在l上方且到l的距离为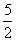 ,过l上的动点P做抛物线的切线,切点分别是C、D,问直线CD是否过定点?试说明理由.
,过l上的动点P做抛物线的切线,切点分别是C、D,问直线CD是否过定点?试说明理由.
20.(本小题满分12分)
已知数列
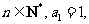 函数
函数
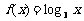
(I)求数列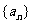 的通项公式;
的通项公式;
(II)设数列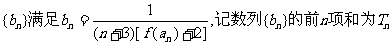 ,试比较
,试比较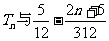 的大小.
的大小.
19.(本小题满分12分)
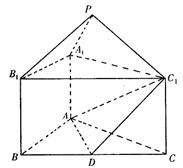
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,D是BC的中点,点P在平面BCC1B1内,PB1=PC1=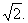
(I)求证:PA1⊥BC; (II)求证:PB1//平面AC1D; (III)求二面角C-AC1-D的大小.
18.(本小题满分12分)
为迎接208年奥运会召开,某工艺品加工厂准备生产具的收藏价值奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”.该厂所用的主要原料为A、B两种贵重金属,已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒,生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒.若奥运会标志每套可获利700元,奥运会吉祥物每套可获利1200元,该厂月初一次性购进原料A、B的量分别为200盒和300盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大利润为多少?
17.(本小题满分12分)
已知函数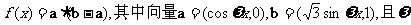 为正实数.
为正实数.
(I)求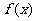 的最大值;
的最大值;
(II)对任意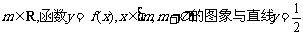 有且仅有一个交点,求
有且仅有一个交点,求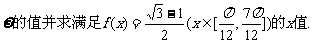
16.给出下列命题:
①如果函数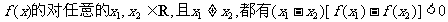 ,则函数
,则函数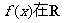 上是减函数;
上是减函数;
②如果函数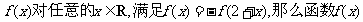 是周期函数;
是周期函数;
③函数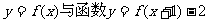 的图象一定不能重合;
的图象一定不能重合;
④对于任意实数x,有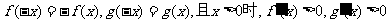 ,则
,则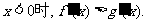
其中正确的命题是 (请将所有正确命题的序号都填上)
15.设函数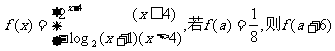 =
.
=
.
14.已知双曲线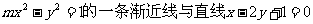 垂直,则双曲线的离心率为
.
垂直,则双曲线的离心率为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com