
2.给定整数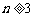 ,证明X={1,2,3,……,
,证明X={1,2,3,……,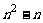 }能写成两个不相交的非空子集的并,使得每一个子集均不包含
}能写成两个不相交的非空子集的并,使得每一个子集均不包含 个元素
个元素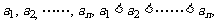 满足
满足
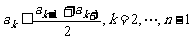
1.设锐角△ABC的三边长互不相等,O为其外心,点A`在线段AO的延长线上,使得∠BA`A=∠CA`A,过A`分别作A` A1⊥AC,A` A2⊥AB,垂足分别为A1,A2,作AHA⊥BC,垂足HA,记△HAA1A2的外接圆半径为RA,类似地可得RB,RC,求证:
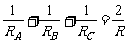
其中R为△ABC的外接圆半径。
(1)对任意正整数n,在平面上是否都存在n个不在同一条直线上的点,使得任意两点间的距离都为正整数?
(2)在平面上是否存在两两不同的无限点列组成的点集M,使得M内所有点不在同一条直线上,且M内任意两点间的距离为正整数?
12.已知椭圆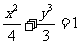 的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是
.
的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是
.
解答题(共4道题,每题15分,满分60分)
11.设向量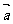 、
、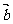 满足|
满足|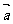 |=1、|
|=1、|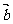 |=2,且
|=2,且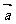 、
、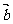 的夹角为60°. 若向量7
的夹角为60°. 若向量7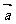 +2t
+2t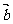 与向量t
与向量t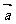 +
+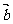 的夹角为钝角,则实数t的取值范围是
.
的夹角为钝角,则实数t的取值范围是
.
9.已知P(2,1)过点P作直线l与x轴、y轴正半轴分别交于A、B两点,则使△AOB(O为坐标原点)的周长最小的直线l的方程是 .
|
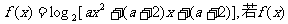 有最大值或最小值,则a的取值范围为
.
有最大值或最小值,则a的取值范围为
.8.所有棱长都等于1的三棱锥的内切球的体积等于 .
本题共有6个小题,要求直接将答案写在题后横线上。
7.已知△ABC是正三角形,P是△ABC所在平面外的一点,且PA=PB=PC,若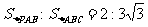 ,则二面角P-AB-C的大小为
.
,则二面角P-AB-C的大小为
.
6.设集合A={1,2,3,4,5,6},一一映射f:A→A满足条件:对任意的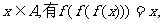 则满足上述条件的映射f的个数为 ( )
则满足上述条件的映射f的个数为 ( )
A.40 B.41 C.80 D.81
5.已知S-ABC是三条棱两两互相垂直的三棱锥,O为底面ABC内一点,若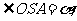
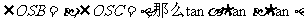 的取值范围是 ( )
的取值范围是 ( )
A.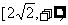 B.
B.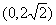 C.
C.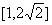 D.
D.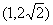
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com