
7.抛物线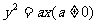 的焦点到其准线的距离是 ( )
的焦点到其准线的距离是 ( )
A.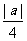 B.
B.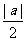 C.
C.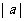 D.
D.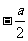
6.各项都是正数的等比数列{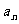 }的公比q≠1,且
}的公比q≠1,且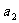 ,
,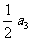 ,
,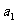 成等差数列,则
成等差数列,则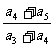 的值为 ( )
的值为 ( )
A
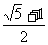 B
B
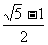 C
C
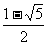 D
D
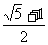 或
或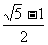
5.长方体AC1中,AA1 = AB = 2,AD = 1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成角的余弦值为 ( )
A.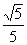 B.
B.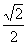 C.
C.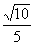 D.0
D.0
4.已知下列命题(其中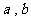 为直线,
为直线,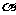 为平面):
为平面):
① 若一条直线垂直于平面内无数条直线,则这条直线与这个平面垂直;
② 若一条直线平行于一个平面,则垂直于这条直线的直线必垂直于这个平面;
③ 若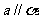 ,
,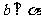 ,则
,则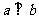 ;
;
④ 若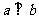 ,则过
,则过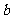 有唯一平面
有唯一平面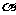 与
与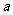 垂直.
垂直.
上述四个命题中,真命题是 ( )
A.①,② B.②,③ C.②,④ D.③,④
3.向量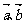 满足
满足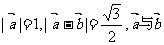 的夹角为60°,则
的夹角为60°,则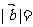 ( )
( )
A.1 B.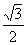 C.
C.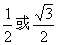 D.
D.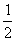
2.双曲线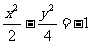 的渐近线方程为 ( )
的渐近线方程为 ( )
A.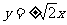 B.
B.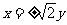 C.
C.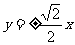 D.
D.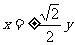
1.已知集合U=R,集合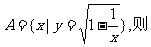
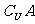 = ( )
= ( )
A.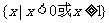 B.
B.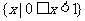
C.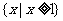 D.
D.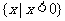
22.本题15分
已知数列{an}满足:a1=a(a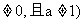 ,其前n项的和Sn=
,其前n项的和Sn=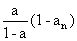
(Ⅰ)求证:{an}为等比数列
(Ⅱ)记bn=anlg|an|(n为正整数),Tn为数列{bn}的前n项和
(1)a=2,求Tn
(2)当a=-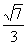 时,是否存在正整数m,使得对于任意的正整数n都有bn³bm?如果存在,求出m的值,否则,说明理由。
时,是否存在正整数m,使得对于任意的正整数n都有bn³bm?如果存在,求出m的值,否则,说明理由。
21.(本题15分)
函数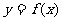 是定义在R上的偶函数,且对任意实数x,都有
是定义在R上的偶函数,且对任意实数x,都有
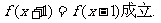 已知当
已知当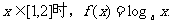
(1)求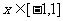 时,函数
时,函数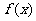 的表达式;
的表达式;
(2)求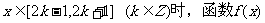 的解析式;
的解析式;
(3)若函数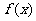 的最大值为
的最大值为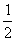 ,在区间[-1,3]上,解关于x的不等式
,在区间[-1,3]上,解关于x的不等式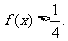
20.(本题14分)
已知函数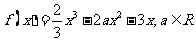 .
.
(1)当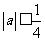 时,证明
时,证明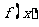 在
在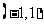 内是减函数;
内是减函数;
(2)若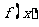 在
在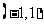 内有且只有一个极值点,求正数
内有且只有一个极值点,求正数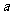 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com