
22.(本小题满分14分)设抛物线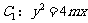
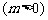 的准线与
的准线与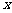 轴交于
轴交于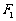 ,焦点为
,焦点为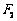 ;以
;以 为焦点,离心率
为焦点,离心率 的椭圆
的椭圆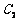 与抛物线
与抛物线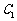 的一个交点为
的一个交点为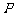 .
.
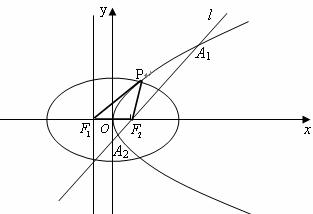
(Ⅰ)当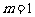 时,求椭圆的方程及其右准线的方程;
时,求椭圆的方程及其右准线的方程;
(Ⅱ)在(Ⅰ)的条件下,直线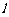 经过椭圆
经过椭圆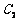 的右焦点
的右焦点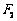 ,与抛物线
,与抛物线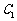 交于
交于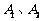 ,如果弦长
,如果弦长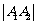 等于△
等于△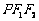 的周长,求直线
的周长,求直线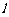 的斜率;
的斜率;
(Ⅲ)是否存在实数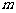 ,使得△
,使得△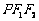 的边长是连续的自然数.
的边长是连续的自然数.
21.(本小题满分14分)数列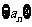 满足
满足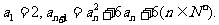
(Ⅰ) 设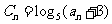 ,求证
,求证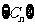 是等比数列;
是等比数列;
(Ⅱ) 求数列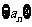 的通项公式;
的通项公式;
(Ⅲ)设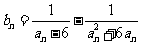 ,数列
,数列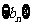 的前
的前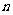 项和为
项和为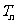 ,求证:
,求证: 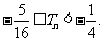
20. (本小题满分12分)已知函数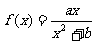 ,在
,在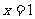 处取得极值为2。
处取得极值为2。
(Ⅰ)求函数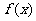 的解析式;
的解析式;
(Ⅱ)若函数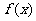 在区间(m,2m+1)上为增函数,求实数m的取值范围;
在区间(m,2m+1)上为增函数,求实数m的取值范围;
(Ⅲ)若P(x0,y0)为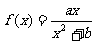 图象上的任意一点,直线l与
图象上的任意一点,直线l与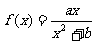 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.
19.(本小题满分12分)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面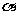 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在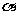 的上方,分别以△
的上方,分别以△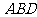 与△
与△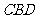 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
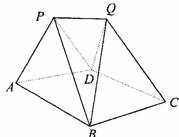
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离.
18.(本小题满分12分)有甲、乙两个篮球运动员,每人各投篮三次,甲三次投篮命中率均为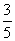 ;乙第一次在距离8米处投篮命中率为
;乙第一次在距离8米处投篮命中率为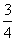 ,若第一次投篮未中,则乙进行第二次投篮,但距离为12米,如果又未中,则乙进行第三次投篮,并且在投篮时距离为16米,乙若投中,则不再继续投篮,且知乙命中的概率与距离的平方成反比.
,若第一次投篮未中,则乙进行第二次投篮,但距离为12米,如果又未中,则乙进行第三次投篮,并且在投篮时距离为16米,乙若投中,则不再继续投篮,且知乙命中的概率与距离的平方成反比.
|
(Ⅱ)求乙投篮命中的概率.
17.(本小题满分12分)已知向量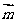
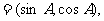
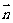
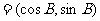 ,
, 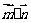
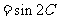 且
且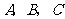 分别为△ABC的三边a,b,c所对的角.
分别为△ABC的三边a,b,c所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA, sinC, sinB成等比数列,
且 , 求c的值.
, 求c的值.
16.若函数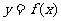 在
在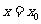 处满足关系⑴
处满足关系⑴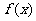 在
在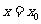 处连续⑵
处连续⑵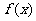 在
在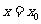 处的导数不存在,就称
处的导数不存在,就称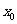 是函数
是函数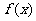 的一个“折点”。下列关于“折点”的四个命题
的一个“折点”。下列关于“折点”的四个命题
①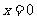 是
是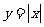 的折点;
的折点;
②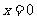 是
是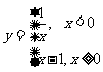 的折点;
的折点;
③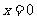 是
是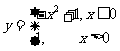 的折点;
的折点;
④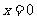 是
是 的折点;
的折点;
其中正确命题的序号是 .
15.如果实数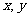 满足
满足 ,目标函数
,目标函数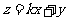 的最大值为12,最小值为3,那么实数
的最大值为12,最小值为3,那么实数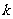 的值为 .
的值为 .
14.设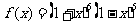 ,则函数
,则函数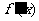 中
中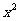 的系数为_______________.
的系数为_______________.
13.已知函数图象 与
与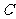 :
: 关于直线
关于直线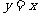 对称,且图象
对称,且图象 关于
关于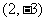 对称,则
对称,则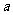 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com