
2、函数y=(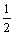 )x与函数y= -
)x与函数y= -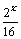 的图象关于( )
的图象关于( )
A.直线x=2对称 B.点(4,0)对称
C.直线x=4对称 D.点(2,0)对称
1、定义集合M与N的新运算,M+N=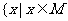 或
或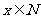 且
且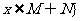 ,则(M+N)+N等于( )
,则(M+N)+N等于( )
A、 B、
B、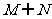 C、M D、N
C、M D、N
22、(本小题满分14分)
已知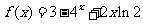 ,数列
,数列 满足:
满足: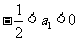 ,
,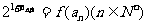 .
.
(Ⅰ)求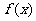 在
在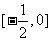 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)求证:  ;
;
(Ⅲ)判断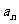 与
与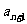
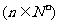 的大小,并说明理由.
的大小,并说明理由.
21.(本小题满分12分)
已知直线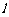 过椭圆E:
过椭圆E: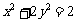 的右焦点
的右焦点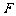 ,且与E相交于
,且与E相交于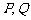 两点.
两点.
① 设 (
(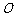 为原点),求点
为原点),求点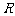 的轨迹方程;
的轨迹方程;
② 若直线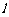 的倾斜角为
的倾斜角为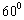 ,求
,求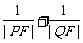 的值.
的值.

20.(本小题满分12分)
已知函数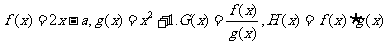
(Ⅰ)当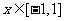 ,求使
,求使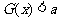 恒成立的
恒成立的 的取值范围;
的取值范围;
(Ⅱ)设方程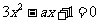 的两根为
的两根为 ,且函数H(x)在区间
,且函数H(x)在区间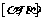 上的最大值比最小值大8,求
上的最大值比最小值大8,求 的值。
的值。
19、(本小题满分12分)已知Rt△ABC中, ,AB=1,BC=2,D为BC的中点,将△ADB沿AD折起,使点B在△ADC所在平面的射影E在AC上.
,AB=1,BC=2,D为BC的中点,将△ADB沿AD折起,使点B在△ADC所在平面的射影E在AC上.
(Ⅰ)求证:CD⊥平面BDE;
(Ⅱ)求折起后二面角B―AD―C的大小;
(Ⅲ)求折起后AB与平面BDE所成的角.

18. (本小题满分12分)某旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
17.(本小题满分12分)已知函数 的图象经过点
的图象经过点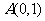 ,
,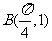 ,且当
,且当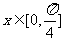 时,
时,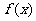 的最大值是2
的最大值是2 -1.
-1.
(1)求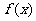 的解析式;
的解析式;
(2)求出满足条件的一个 ,使得将
,使得将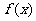 的图象按向量
的图象按向量 平移后可以得到一个奇函数的图象.
平移后可以得到一个奇函数的图象.
16、对于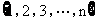 和它的每个非空子集,我们定义“交替和”如下:把子集中的所有数按从大到小的顺序排列,然后从最大的数开始交替地加减各数(例如:
和它的每个非空子集,我们定义“交替和”如下:把子集中的所有数按从大到小的顺序排列,然后从最大的数开始交替地加减各数(例如: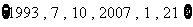 的交替和是
的交替和是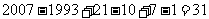 ,而
,而 的交替和是5)。那么,当
的交替和是5)。那么,当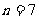 时,所有这些交替和的总和是 。
时,所有这些交替和的总和是 。
15、设 ,要使函数
,要使函数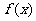 在
在 内连续,则
内连续,则 的值为
。
的值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com