
4.6人排成一排,甲乙两人中间至少有一个人的排法的概率是 ( )
A.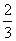 B.
B.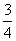 C.
C. D.
D.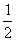
3.若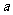 2+b2-2c2=0,则直线a
2+b2-2c2=0,则直线a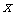 +by+c=0被
+by+c=0被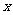 2+y2=1所截得的弦长为 ( )
2+y2=1所截得的弦长为 ( )
A.1 B.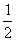 C.
C.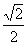 D.
D.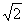
2.已知sin(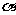 一
一 )=
)= ,则cos(
,则cos( +
+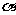 )的值等于 ( )
)的值等于 ( )
A.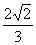 B.一
B.一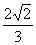 C.一
C.一 D.
D.
1.集合P={(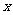 ,y)|y=k,
,y)|y=k,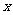
 R},Q={(
R},Q={(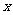 ,y)|y=
,y)|y=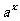 +1,
+1,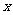 ∈R,
∈R,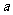 >0,且
>0,且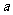 ≠l},已知P
≠l},已知P Q=
Q=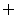 ,那么实数k的取值范围是 ( )
,那么实数k的取值范围是 ( )
A.(一∞,l) B.(一∞,l]
C.(1,+∞) D.(一∞,+∞)
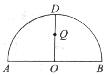
21.(本小题满分l4分)如图所示,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线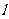 与曲线C相交于不同的两点M、N,且M在D、N之间,设
与曲线C相交于不同的两点M、N,且M在D、N之间,设 ,求
,求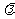 的取值范围.
的取值范围.
20.(本小题满分13分)等比数列{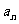 }中,首项
}中,首项 >1,公比q>0,且
>1,公比q>0,且 ,
, ,
,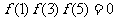 .
.
(1)求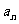 ;
;
(2)若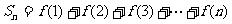 ,求
,求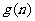 =
= 取最大值时
取最大值时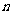 的值.
的值.
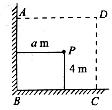
19.(本小题满分12分)用长为16 m的篱笆,借助墙角围成一矩形ABCD草坪,在P处有一棵树与两墙的距离分别是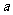 m(0<
m(0<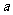 <12)和4 m.若将此树圈进去,求矩形草坪ABCD面积的最大值M.
<12)和4 m.若将此树圈进去,求矩形草坪ABCD面积的最大值M.
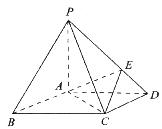
18.(本小题满分12分)如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=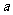 ,PB=PD=
,PB=PD=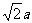 .点E在PD上,且PE:ED=2:1.
.点E在PD上,且PE:ED=2:1.
(1)求证:PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角 的大小;
的大小;
(3)在棱PC上是否存在一点F,使BF//平面AEC,并证明你的结论.
17.(本小题满分12分)已知向量 ,
, ,记
,记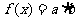 .
.
(1)求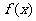 的值域及最小正周期;
的值域及最小正周期;
(2)若 ,其中
,其中 ,求角
,求角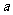 .
.
16.(本小题满分12分)有A、B两个口袋,A袋中装有4个白球、2个黑球,B袋中装有3个白球、4个黑球.从A、B两袋中各取2个球交换后,求A袋中装有4个白球的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com