
20.(本小题满分l3分)如图所示,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=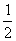 AD=
AD=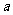 ,G为EF的中点,
,G为EF的中点,
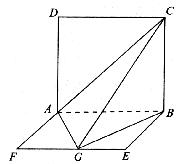
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值;
(3)求二面角B-AC-G的大小.
19.(本小题满分12分)已知数列 中任意相邻两项
中任意相邻两项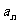 、
、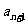 都是方程
都是方程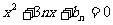 的两根,
的两根,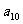 =-l7,求:
=-l7,求:
(1)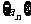 的通项公式;
的通项公式;
(2)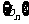 的通项公式.
的通项公式.
18.(本小题满分12分)某地区的一种特色水果上市时间能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌现象,现有三种价格模拟函数:
①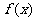 =
=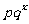 ;
;
②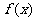 =
=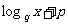 ;
;
③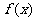 =
= .(以下三式中
.(以下三式中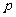 、
、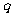 均为常数,且
均为常数,且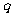 >2)
>2)
(1)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(2)若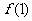 =4,
=4,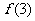 =6,求出所选函数
=6,求出所选函数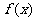 的解析式(注:函数的定义域是[1,6].其中
的解析式(注:函数的定义域是[1,6].其中 =1表示4月1日,
=1表示4月1日, =2表示5月1日……以此类推).
=2表示5月1日……以此类推).
(3)试问:在(2)的条件下,这种水果在几月份价格下跌?
17.(本小题满分12分)甲、乙两人进行羽毛球比赛,在每一局中,甲获胜的概率为P(0<P<1).
(1)如果甲、乙两人共比赛4局,甲恰好负2局的概率不大于其恰好胜3局的概率,试求P的取值范围;
(2)若P=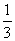 ,当采用3局2胜制的比赛规则时,求甲获胜的概率;
,当采用3局2胜制的比赛规则时,求甲获胜的概率;
(3)如果甲、乙两人比赛6局,那么甲恰好胜3局的概率可能是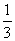 吗?为什么?
吗?为什么?
16.(本小题满分12分)已知二次函数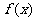 对任意
对任意 ∈R,都有
∈R,都有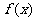 <0且,
<0且,
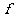 (1-
(1- )=
)=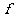 (1+
(1+ )成立,设向量
)成立,设向量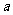 =(sin
=(sin ,2)、b=(2sins
,2)、b=(2sins ,
,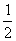 )、c=(cos2
)、c=(cos2 ,1)、d=(1,2),当
,1)、d=(1,2),当 是三角形内角时,求不等式
是三角形内角时,求不等式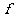 (
(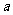 ·b)>
·b)> 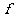 (c·d)的解集.
(c·d)的解集.
15.购买一件售价为5000元的电子产品,采用分期付款办法,每期等额付款,分6个月付清,如果月利率为0.8%,每月利息按复利计算,则每期应付款___________元.(答案四舍五入到整数,参考数据:1.085=1.4693,1.086=1.5868,1.087=1.7138,1.0085=1.9406,1.0086=1.0489,1.0087=1.0573)
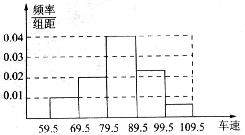
14.在某路段检查站监控录像显示,在某时段内,有l000辆汽车通过该站,现随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如图所示的频率分布直方图,则估计在这一时段内通过该站的汽车中车速不小于90km/h的约有___________辆.(注:分析时车速均取整数)
13.过双曲线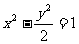 的右焦点作直线
的右焦点作直线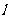 交双曲线于A、B两点,若使得|AB|=
交双曲线于A、B两点,若使得|AB|=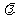 (
(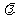 ∈R)的直线
∈R)的直线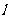 恰有3条,则
恰有3条,则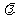 的值是___________.
的值是___________.
12.湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下一个直径为12cm,深2cm的空穴,则该球的表面积为___________cm2.
11. ∈(0,
∈(0,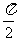 ),则函数
),则函数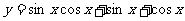 的值域是_________________。
的值域是_________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com