
5. 在等差数列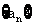 中,公差d=1,
中,公差d=1,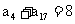 ,则
,则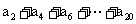 的值为(
)
的值为(
)
A.40 B.45 C.50 D.55
4.设函数f(x)是定义在R上的以3为周期的奇函数,若f(1)>1,f(2)=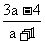 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.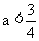 B.
B.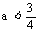 且
且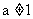 C.
C.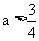 或
或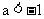 D.
D.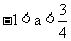
3.若A、B、C是锐角三角形ABC的三个内角,向量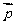 =(sinA,cosA),
=(sinA,cosA), =(sinB,−cosB),则
=(sinB,−cosB),则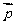 与
与 的夹角为( )
的夹角为( )
A.锐角 B.直角 C.钝角 D.以上都不对
2.函数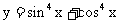 的最小正周期是( )
的最小正周期是( )
A.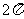 B.
B.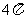 C.
C. 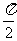 D.
D.

1.已知集合M=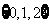 ,N=
,N=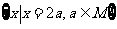 ,则集合
,则集合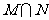 =( )
=( )
A、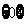 B、
B、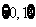 C、
C、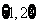 D、
D、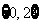
17(本题12分).已知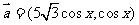 ,
,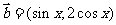 ,记函数
,记函数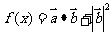
(1)求函数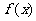 的最小正周期及最值;
的最小正周期及最值;
(2)当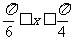 时,求函数
时,求函数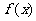 的值域.
的值域.
18(本题12分).甲、乙两人同时参加一次面试,已知在备选的10道试题中,甲能答对其中的6道,乙能答对其中的8道,规定每次考试都从备选题中随机抽出3道题进行测试,至少答对2道题才算通过。求:
(Ⅰ)甲答对两道题的概率;
(Ⅱ)甲、乙两人至少有一人通过面试的概率.
19(本题12分).如图,在四棱锥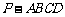 中,底面
中,底面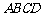 是一直角梯形,
是一直角梯形,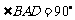 ,
,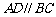 ,
,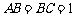 ,
,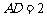 ,且
,且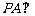 平面
平面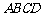 ,
,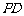 与底面成
与底面成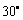 角.
角.
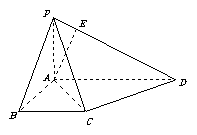
(Ⅰ) 求证:平面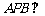 平面
平面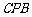 ;
;
(Ⅱ) 求二面角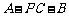 的一个三角函数值;
的一个三角函数值;
20(本题12分).设函数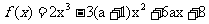 ,其中
,其中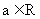
(Ⅰ)若f(x)在x=3处取得极值,求常数a 的值;
(Ⅱ)若f(x)在 上为增函数,求a的取值范围
上为增函数,求a的取值范围
21(本题12分).已知数列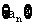 的前n项和
的前n项和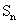 满足
满足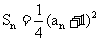 ,且
,且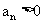
(1) 求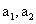 ;
;
(2) 求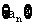 的通项公式;
的通项公式;
(3)令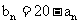 ,问数列
,问数列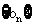 的前多少项的和最大?
的前多少项的和最大?
22(本题14分).在直角坐标系中,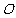 为坐标原点,设直线
为坐标原点,设直线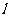 经过点
经过点
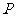 (3,
(3,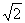 ),且与
),且与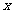 轴交于点
轴交于点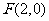
(1)求直线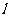 的方程;
的方程;
(2)若一个椭圆经过点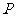 ,且以点
,且以点 为它的一个焦点,求椭圆的标准方程;
为它的一个焦点,求椭圆的标准方程;
(3)若在(1)(2)的情况下,设直线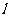 与椭圆的另一个交点
与椭圆的另一个交点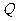 ,且
,且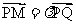 ,
,
当|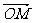 |最小时,求
|最小时,求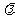 对应值.
对应值.
16.已知m、n为直线,α,β为平面,给出下列命题:
①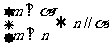 ②
②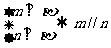 ③
③ ④
④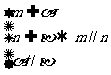
其中的正确命题序号是:
15.若一个圆的圆心在抛物线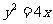 的焦点上,且此圆与直线
的焦点上,且此圆与直线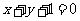 相切,则这个圆的方程是 ;
相切,则这个圆的方程是 ;
14.已知n为等差数列−4,−2,0,…,中的第8项,则二项式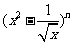 展开式中的常数项是 ;
展开式中的常数项是 ;
13.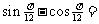 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com