
21.(本题15分)设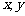 为正实数,
为正实数,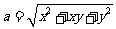 ,
,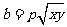 ,
,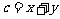 .
.
(Ⅰ)如果 ,则是否存在以
,则是否存在以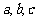 为三边长的三角形?请说明理由;
为三边长的三角形?请说明理由;
(Ⅱ)对任意的正实数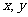 ,试探索当存在以
,试探索当存在以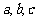 为三边长的三角形时
为三边长的三角形时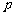 的取值范围.
的取值范围.
20.(本题14分)已知数列{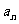 }、{
}、{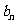 }满足:
}满足: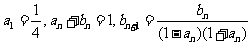 .
.
(Ⅰ)求 ;
;
(Ⅱ)设 ,求数列
,求数列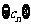 的通项公式;
的通项公式;
(Ⅲ)设 ,不等式
,不等式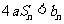 恒成立时,求实数
恒成立时,求实数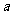 的取值范围.
的取值范围.
19.(本题14分)已知 为坐标原点,
为坐标原点, ,
, .
.
(Ⅰ)求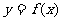 的单调递增区间;
的单调递增区间;
(Ⅱ)若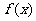 的定义域为
的定义域为 ,值域为
,值域为 ,求
,求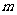 的值.
的值.
18.(本题14分)某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(Ⅰ)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(Ⅱ)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为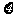 ,求随机变量
,求随机变量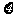 的分布列和数学期望.
的分布列和数学期望.
17.给出下列四个结论:
①命题 的否定是“
的否定是“ ”;
”;
②“若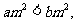 则
则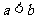 ”的逆命题为真;
”的逆命题为真;
③函数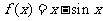 (x
(x )有3个零点;
)有3个零点;
④对于任意实数x,有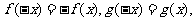 且x>0时,
且x>0时, 则x<0时
则x<0时
其中正确结论的序号是 .(填上所有正确结论的序号)
|
16.数列 中,
中, ,若对任意的正整数
,若对任意的正整数 ,
,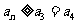 都成立,则
都成立,则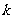 的取值范围为 .
的取值范围为 .
15.已知函数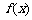 的导函数
的导函数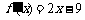 ,且
,且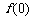 的值为整数,当
的值为整数,当 时,
时,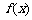 所有可能取的整数值有且只有1个,则
所有可能取的整数值有且只有1个,则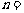 .
.
14.等比数列 的前
的前 项和为
项和为 ,已知
,已知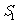 ,
, ,
, 成等差数列,则
成等差数列,则 的公比为 .
的公比为 .
13.已知 ,则
,则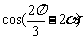 的值等于 .
的值等于 .
12.如果执行下面的程序框图,那么输出的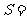 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com