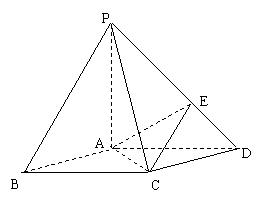
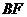
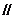（Ⅲ）在棱上是否存在一点，使平面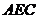？证明你的结论.

本小题主要考查了棱锥、直线与平面垂直的判定与性质，二面角及二面角的平面角、直线与平面平行的判定和性质，同时考查了利用空间向量解决立体几何问题的转换能力、一定的计算能力以及逻辑推理能力.

 第3问在设问上有一定开放性，这对空间观念的要求，对空间图形转换要求，在水平层次上就有较大的提高，切入点是从特殊点开始进行探究.

此题可用空间向量法解决，关键是能合理的构建空间坐标系.

   总之，本题在解决方法上利用向量手段解决几何问题，很好地体现了数学的和谐美。同时，空间向量在立体几何中的应用为考生创造了几何证明的新思路，体现了解决问题策略的多样化。另外，本题通过开放性问题的设计，给学生留出了较大的思维空间，为学生灵活运用所学知识解决问题建立了一个平台.

（II）求以为棱，与为面的二面角的大小；

（I）证明平面；   

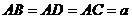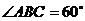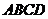（4）如图，在底面是菱形的四棱锥中，，，,点在上，且.

所以

答：耕地平均每年至多减少4公顷.

得