
6. 如图,函数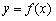 的图象在点P处的切线方程是
的图象在点P处的切线方程是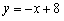 ,则
,则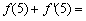 ( )
( )
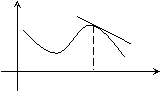 A.
A.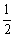 B.1
B.1 
C.2 D.0
5. 函数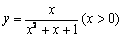 的值域是( )
的值域是( )
A.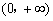 B.
B.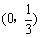 C.
C.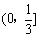 D.
D.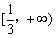

4. 函数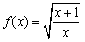 的定义域为( )
的定义域为( )
A.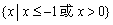 B.
B.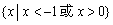

C.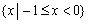 D.
D.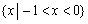

3. 函数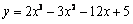 在区间[0,3]上的最大值与最小值为( )
在区间[0,3]上的最大值与最小值为( )
A.5,– 15 B.5,– 4 C.– 4,– 15 D.5,– 16
2. 在等比数列{an}中,已知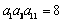 ,则
,则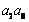 等于( )
等于( )
A.16 B.6 C.12 D.4
1. 已知集合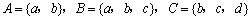 ,那么集合
,那么集合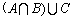 等于( )
等于( )
A.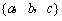 B.
B.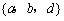

C.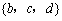 D.
D.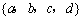

2、 《练习册》 P 30
四、 小结
二次函数是一种解决现实生活问题的好方法,我们要运用二次函数的知识求出实际问题的最大值,分析和表示实际问题中变量之间的二次函数关系。解决此类问题时,要特别注意审清题目,理解题意。
五、 作业
书本 P 61 习题2.7 1
六、 教学后记
1、 书本 P 60 随堂练习
2、 能够分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大值,发展解决问题的能力
教学重点和难点
重点:运用二次函数的知识求出实际问题的最大值
难点:运用二次函数的知识求出实际问题的最大值
教学过程设计
一、 从学生原有的认知结构提出问题
做生意的时候,我们都常常会考虑如何才能获得最大利润。这节课,我们利用二次函数,求如何才能获得最大利润。
二、 师生共同研究形成概念
1、 书本引例
此例子是利用二次函数解决问题。这类问题都比较抽象,建议教学时要向学生说清道理,逐个问题分析。若学生不理解书本的方法,可以考虑第二种方法。
☆ 书本解法 设销售单价为x元时,那么
(1)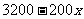 ;
;
(2)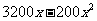 ;
;
(3)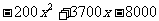 ;
;
(4)9.25元、9112.5元。
☆ 解法二 设销售单价降低x元时,那么
(1) 单件销售利润可以表示为 ;
(2) 销售总量可以表示为 ;
(3) 总利润可以表示为 ;
(4) 当销售单价是 元时,可以获得最大利润,最大利润是 。
2、 做一做 P 46
☆ 做一做 书本P 59 做一做
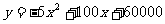 。
。
☆ 议一议 书本P 60 议一议
(1) 当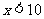 时,橙子的总产量随增种橙子树的增加而增加;当
时,橙子的总产量随增种橙子树的增加而增加;当 时,橙子的总产量随增种橙子树的增加而减少。
时,橙子的总产量随增种橙子树的增加而减少。
(2) 增种6 ~ 14棵,都可以使橙子总产量在60400个以上。
3、 讲解例题
例1 《练习册》 P 30 9
分析:此例可以先由学生单独完成,然后老师作适当提点。
三、 随堂练习
1、 经历探索T恤衫销售中最大利润等问题的过程,体会二次函数是一类最优化问题的数学模型,并感受数学的应用价值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com