
1. 在△ABC中,如果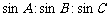 =2∶3∶4,那么cosC等于( D ).
=2∶3∶4,那么cosC等于( D ).
A.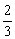 B.
B.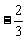 C.
C.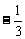 D.
D.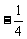
2.利用余弦定理,可以解决以下两类解斜三角形的问题:
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其他两个角.
[精典范例]

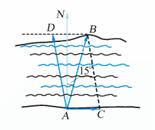 [例1]在长江某渡口处,江水以
[例1]在长江某渡口处,江水以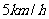 的速度向东流,一渡船在江南岸的
的速度向东流,一渡船在江南岸的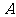 码头出发,预定要在
码头出发,预定要在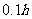 后到达江北岸
后到达江北岸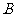 码头,设
码头,设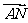 为正北方向,已知
为正北方向,已知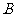 码头在
码头在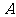 码头的北偏东
码头的北偏东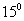 ,并与
,并与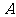 码头相距
码头相距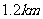 .该渡船应按什么方向航行?速度是多少(角度精确到
.该渡船应按什么方向航行?速度是多少(角度精确到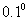 ,速度精确到
,速度精确到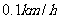 )?
)?
[解]如图,船按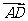 方向开出,
方向开出,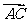 方向为水流方向,以
方向为水流方向,以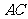 为一边、
为一边、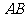 为对角线作平行四边形
为对角线作平行四边形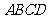 ,其中
,其中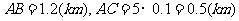 .
.
在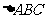 中,由余弦定理,得
中,由余弦定理,得
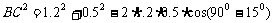 所以
所以 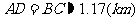 .
.
因此,船的航行速度为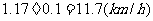 .
.
在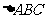 中,由正弦定理,得
中,由正弦定理,得 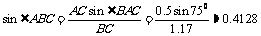 所以
所以 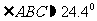
所以 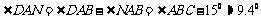
答:渡船应按北偏西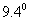 的方向,并以
的方向,并以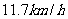 的速度航行.
的速度航行.
[例2]在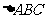 中,已知
中,已知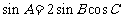 ,试判断该三角形的形状.
,试判断该三角形的形状.
[解]由正弦定理及余弦定理,得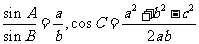 ,
,
所以 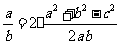 ,整理得
,整理得 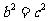
因为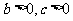 ,所以
,所以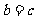 .因此,
.因此,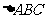 为等腰三角形.
为等腰三角形.
[例3]如图,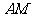 是
是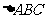 中
中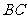 边上的中线,求证:
边上的中线,求证: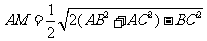 .
.
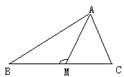 [证明]
[证明]
设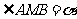 ,则
,则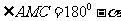 .在
.在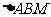 中,由余弦定理,得
中,由余弦定理,得
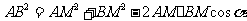 .
.
在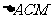 中,由余弦定理,得
中,由余弦定理,得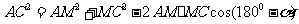 因为
因为
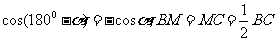 ,
,
所以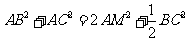 ,
,
因此,
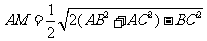 .
.
追踪训练一
1.余弦定理:
(1)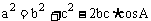 ,
,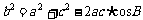 ,
,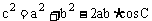 .
.
(2) 变形: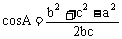 ,
,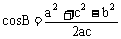 ,
,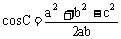
3.初步利用定理判断三角形的形状。
[课堂互动]
自学评价
2.余弦定理的教学要达到“记熟公式”和“运算正确”这两个目标;
1.能把一些简单的实际问题转化为数学问题;
4、
△ABC中,若 ,
,
则A= 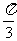 。
。
|

3.在△ABC中,若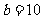 ,
,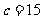 ,C=
,C=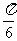 ,则此三角形有 一 解。
,则此三角形有 一 解。
提示:由余弦定理得:

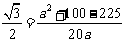
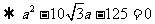
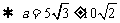
负值不合题意,舍去。
2.在△ABC中,已知AB=5,AC=6,BC=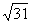 ,则A= ( A )
,则A= ( A )
A
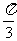 B
B 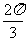 C
C 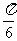 D
D 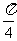
1.在△ABC中,已知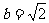 ,
,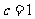 ,B=
,B=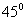 ,则
,则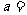 ( B )
( B )
A 2
B 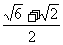
 C
C  D
D 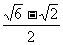
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com