
4. 如图,△ABC是简易遮阳棚,A、B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为了使遮阴影面ABD面积最大,遮阳棚ABC与地面所成的角为( )
如图,△ABC是简易遮阳棚,A、B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为了使遮阴影面ABD面积最大,遮阳棚ABC与地面所成的角为( )
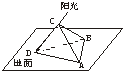
A.75° B.60° C.50° D.45
3.已知△ABC中,a∶b∶c=1∶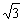 ∶2,则A∶B∶C等于( )
∶2,则A∶B∶C等于( )
A.1∶2∶3 B.2∶3∶1 C.1∶3∶2 D.3∶1∶2
2.在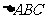 中,若
中,若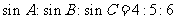 ,且
,且 ,则
,则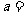 ,
,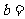 ,
,
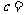 .
.
1.在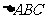 中,
中,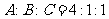 ,则
,则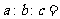 ( )
( )
A.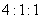 B.
B.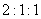
C.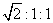 D.
D.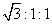
3. 在△ABC中,若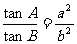 ,则△ABC的形状是( )
,则△ABC的形状是( )
A.直角三角形 B.等腰或直角三角形
C.不能确定 D.等腰三角形
[选修延伸]
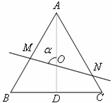
[例4]如图所示,在等边三角形中,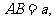
 为三角形的中心,过
为三角形的中心,过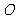 的直线交
的直线交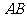 于
于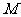 ,交
,交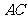 于
于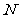 ,
,
求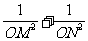 的最大值和最小值.
的最大值和最小值.
 [解]
[解]
追踪训练二
2. 在△ABC中,若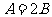 ,则
,则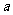 等于( )
等于( )
A.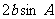 B.
B.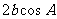
C.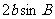 D.
D.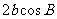
1. 在△ABC中,已知b = 6,c = 10,B = 30°,则解此三角形的结果是 ( )
A.无解 B.一解
C.两解 D.解的个数不能确定
2.三角形的面积公式:
(1)s=_______=_______=_______
(2)s=__________________
(3)s=____________
[精典范例]
[例1]在△ABC中,已知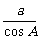 =
=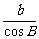 =
=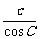 ,试判断△ABC的形状.
,试判断△ABC的形状.
[解]
点评: 通过正弦定理,可以实现边角互化.
 [例2]在△ABC中,AD是∠BAC的平分线,用正弦定理证明
[例2]在△ABC中,AD是∠BAC的平分线,用正弦定理证明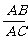 =
=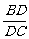 .
.
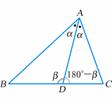 [证]
[证]
[例3]根据下列条件,判断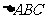 有没有解?若有解,判断解的个数.
有没有解?若有解,判断解的个数.
(1)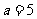 ,
,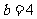 ,
,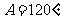 ,求
,求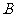 ;
;
(2)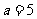 ,
,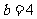 ,
,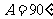 ,求
,求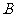 ;
;
(3)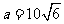 ,
,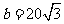 ,
,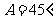 ,求
,求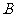 ;
;
(4)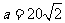 ,
,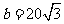 ,
,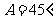 ,求
,求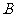 ;
;
(5)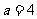 ,
,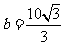 ,
,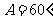 ,求
,求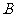 .
.
[解]
追踪训练一
1.正弦定理:在△ABC中,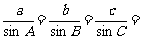
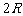 ,
,
2R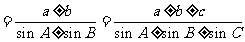
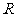 为
为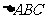 的_______________
的_______________
3.判断△ABC的形状.
[课堂互动]
自学评价
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com