2. 运用基本不等式求解函数最值问题．

[课堂互动]

自学评价

1. 理解最值定理的使用条件：

一正二定三相等．

4．已知a , b , c不全相等的三个正数, 且abc=1 , 求证: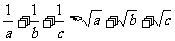

注意：利用基本不等式证明时要交代等号为何不能成立．

3．已知a+b+c=1,求证a²+b²+c²≥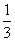

提示：只要证3(a²+b²+c²)≥1即可．

2．已知a>1求证a+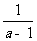≥3

略证．

1．设P为正数，求下列各组数的算术平均数与几何平均数．

(1)2与8　　　答案：5，4

(2)3与12　　答案：7.5，6

(3)P与9P　　答案：5p，3p

(4)2与2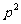　　答案：p²+1，2p

2．基本不等式的推广：n个(n>1)非负数的几何平均数不大于它们的算术平均数．即若a_i≥0(i=1,2,…,n),则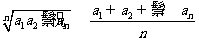(n>1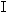,nN)

追踪训练

1.上面两例在于：(1)揭示基本不等式的内容与证法．(2)举例说明利用基本不等式证题的方法技巧，以让学生初步领会不等式证明的基本方法．

3．注意严格不等式的证明方法．

思维点拔：

5.基本不等式的几何解释：半径不小于半弦．

例2. 利用基本不等式证明下列不等式：

(1)　　 已知a>0,求证 a+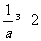

　　 (2).已知a, b, c∈R , 求证: a²+b²+c²≥ab+bc+ac .

(3).已知x , y , z是互不相等的正数, 且x+y+z=1 , 求证: (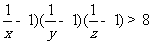

证明：因为题目简单，证略．

点评：1..基本不等式的变形公式：

(1)

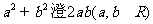
(2) 　

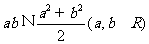
(3) 　

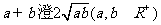
(4)