
1.(2000年上海高考)已知复数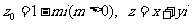
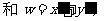
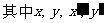 均为实数,
均为实数,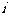 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数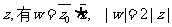 .
.
(Ⅰ)试求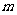 的值,并分别写出
的值,并分别写出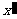 和
和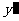 用
用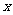 、
、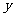 表示的关系式;
表示的关系式;
(Ⅱ)将(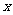 、
、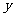 )作为点
)作为点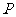 的坐标,(
的坐标,(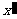 、
、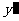 )作为点
)作为点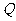 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点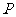 变到这一平面上的点
变到这一平面上的点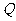 ,当点
,当点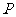 在直线
在直线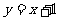 上移动时,试求点
上移动时,试求点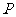 经该变换后得到的点
经该变换后得到的点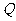 的轨迹方程;
的轨迹方程;
(Ⅲ)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由.
1.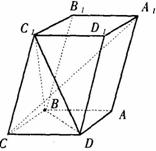 (2000年全国高考题)如图,已知平行六面体ABCD-
(2000年全国高考题)如图,已知平行六面体ABCD-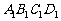 的底面ABCD是菱形,且
的底面ABCD是菱形,且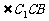 =
=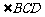 =
=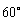 .
.
(I)证明: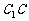 ⊥BD;
⊥BD;
(II)假定CD=2,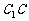 =
=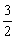 ,记面
,记面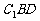 为
为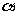 ,面CBD为
,面CBD为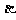 ,求二面角
,求二面角 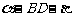 的平面角的余弦值;
的平面角的余弦值;
(III)当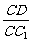 的值为多少时,能使
的值为多少时,能使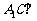 平面
平面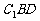 ?请给出证明.
?请给出证明.
4.(2000年全国高考18题)略.
[答案与提示:1.满足AC^BD的任一条件均可; 2.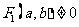 /
/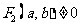 ,/
,/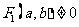 且
且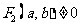 /
/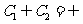 /
/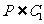 等; 3.侧棱相等/侧棱与底面所成角相等/……]
等; 3.侧棱相等/侧棱与底面所成角相等/……]
;(Ⅰ);(Ⅱ);(Ⅲ).
3.(2002年上海高考)
命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥.命题A的等价命题B可以是:底面为正三角形,且 的三棱锥是正三棱锥.
2.(2002上海春季高考)设曲线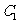 和
和 的方程分别为
的方程分别为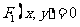 和
和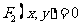 ,则点
,则点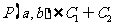 的一个充分条件为_____________________.
的一个充分条件为_____________________.
1.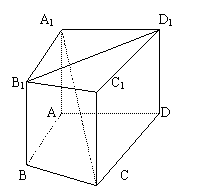 (1998年全国高考)如图, 在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件__________时, 有A1C^B1D1.(注:填上一种你认为正确的一种条件即可, 不必考虑所有可能的情形.)
(1998年全国高考)如图, 在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件__________时, 有A1C^B1D1.(注:填上一种你认为正确的一种条件即可, 不必考虑所有可能的情形.)
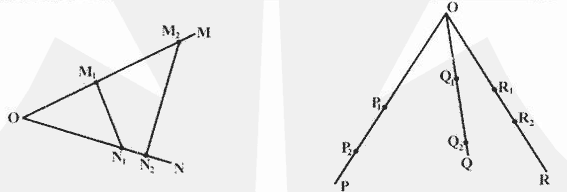
4.(2002年上海春季高考)如下图.若从点O所作的两条射线OM、ON上分别有点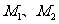 与点
与点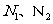 ,则三角形面积之比
,则三角形面积之比 .若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点
.若从点O所作的不在同一平面内的三条射线OP、OQ和OR上,分别有点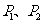 ,点
,点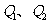 和点
和点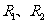 ,则类似的结论为:______________________________.
,则类似的结论为:______________________________.
[答案与提示:1.②③④ ①/①③④
①/①③④ ②;
2.②③; 3.
②;
2.②③; 3.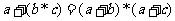 /
/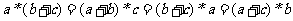 等; 4.
等; 4.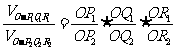 .]
.]
3.(2001年上海春季高考)若记号“*”表示求两个实数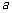 与
与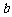 的算术平均数的运算,即
的算术平均数的运算,即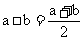 ,则两边均含有运算符号“*”和“+”,且对于任意3个实当选
,则两边均含有运算符号“*”和“+”,且对于任意3个实当选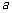 、
、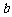 、
、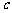 都能成立的一个等式可以是__________________.
都能成立的一个等式可以是__________________.
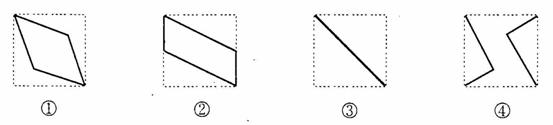
2.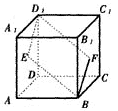 (2000年全国高考)如图,E、F分别为正方体的面
(2000年全国高考)如图,E、F分别为正方体的面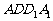 、面
、面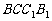 的中心,则四边形
的中心,则四边形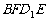 在该正方体的面上的射影可能是_______.(要求:把可能的图的序号都填上)
在该正方体的面上的射影可能是_______.(要求:把可能的图的序号都填上)
1.(1999年全国高考) 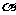 、
、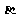 是两个不同的平面,
是两个不同的平面,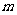 、
、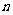 是平面
是平面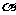 及
及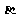 之外的两条不同直线,给出四个论断: ①
之外的两条不同直线,给出四个论断: ①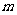 ⊥
⊥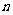 ; ②
; ②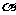 ⊥
⊥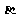 ; ③
; ③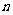 ⊥
⊥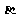 ; ④
; ④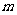 ⊥
⊥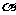 .
.
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:__________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com