1．不等式与方程的关系是关键．从不等式的解方程的根韦达定理(或将根代入) 新不等式的解．

追踪训练一

2．不等式(x-1)(x-a)<0的解集为　当a>1时,(1,a). 当a <1时,(a,1).当a=1时,φ 　。

[精典范例]

例1已知不等式x²+ax+b<0的解集为{x|－1<x<2}, 求不等式bx²－ax+1<0的解集。

[解]

－1，2是方程x²+ax+b＝0的两根，则由韦达定理可求得a=－1,b=－2.再解新不等式得解集为

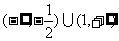
变式：已知不等式b x²－ax+1 <0的解集为{x| x < 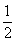－或x>1}, 求不等式x²+ax+b<0的解集．

答案：(1，2)．

思维点拔：

1．不等式a(x-1)(x-2)<0的解集为

{x|x<1或x>2}则a与0的关系为： a<o　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2．会解一些简单的含参数的一元二次不等式．

[课堂互动]

自学评价

1．进一步理解三个一元二次之间的关系，掌握一元二次不等式解的逆向问题。　

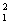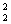4．设k∈R , x₁ , x₂是方程x²－2kx+1－k²=0的两个实数根, 则x+x的最小值为

(　C　)

　 A. -2　 　 B. 0 　 C. 1　　　 D. 2

[选修延伸]

高次不等式的解法

解下列不等式：

(1)

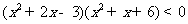
(2)

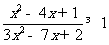
3. 函数y=lg(-x²+5x+24)的值小于1，则x的取值范围为_____________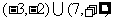

2. 函数y=lg(2x²+3x-1)的定义域为_____________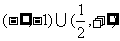

1. 函数y=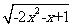的定义域为_____________

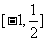5．　　　 学会用化归的思想解决一些可化为一元二次不等式的问题。

追踪训练一