
3.回顾(变量范围与实际情况要一致)
追踪训练
2.解题(设,列,解,答)
1.审题
2.体会由实际问题建立数学模型的过程和方法
[课堂互动]
精典范例
例1.用一根长为100m的绳子能围成一个面积大于600m2的矩形吗? 当长、宽分别为多少米时, 所围成矩形的面积最大?
[解]
见书.
例2. 某小型服装厂生产一种风衣, 日销货量x件与货价P元/件之间的关系为P=160-2x , 生产x件所需成本为C=500+30x元. 问: 该厂日产量多大时, 日获利不少于1300元?
见书.
例3:汽车在行驶中, 由于惯性的作用, 刹车后还要继续向前滑行一段距离才能停住, 我们称这段距离为“刹车距离”, 刹车距离是分析事故的一个重要因素.
在一个限速为40km / h的弯道上 , 甲、乙两辆汽车相向而行 , 发现情况不对 , 同时刹车, 但还是相碰了, 事后现场勘查测得甲车的刹车距离略超过12m , 乙车的刹车距离略超过10m , 又知甲、乙两种车型的刹车距离s ( m )与车速x ( km / h )之间分别有如下关系 : s甲= 0.1x+0.01x2, s乙=0.05x+0.005x2, 问甲、乙两车有无超速现象?
[解]
见书.
思维点拔:
解应用题的步骤:
1.学会建立一元二次不等式及二次函数模型解决实际问题
2.分类讨论不要重复和遗漏.
追踪训练二
方程x2-mx-m+3=0的两根均在(-4,0)内,求m的取值范围.
1.实根分布问题解题步骤
(1)化方程一边为零;
(2)设非零一边为函数f(x);
(3)画函数f(x)的符合题意的草图;
(4)根据草图列不等式组;
(5)解不等式组.
2.已知函数f(x)=ax2+bx+c的图象过点(-1,0)是否存在常数a,b,c使不等式x≤f(x)≤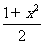 对切实数x都成立?若存在,求出a,b,c的值,若不存在,说明理由.
对切实数x都成立?若存在,求出a,b,c的值,若不存在,说明理由.
解:易知f(1)=1.
于是由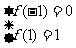 得
得
所以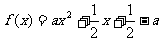
所以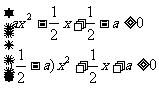 恒成立.
恒成立.
所以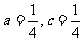 .
.
例2. 分别求m的取值范围, 使方程x2-mx-m+3=0 的两根满足下列条件:
(1)两根都大于-5 ;
(2)一根大于0小于1 , 一根大于1小于2 .
解:设 作草图后得.
作草图后得.
(1) 进而得
进而得

(2)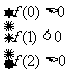 得
得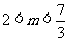
例3:已知A={x|x2+(P+2)x+4=0}, M={x|x>0}, 若A∩M=φ, 求实数P的取值范围.
[解]分A=与A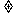 φ两情况,最终可求出
φ两情况,最终可求出 .
.
思维点拔:
1.当a为何值时, 不等式(a2-3a+2) x2+(a-1)x+2>0恒成立.
解: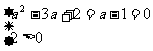 或
或
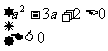
解得: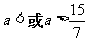
2。若ax2+bx+c>0解集为φ,则
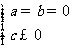 或
或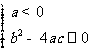
追踪训练一
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com