
1.(2000年全国高考题)如图,已知平行六面体ABCD-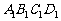 的底面ABCD是菱形,且
的底面ABCD是菱形,且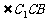 =
=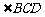 =
=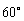 。
。
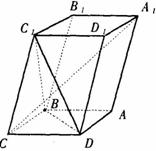 (I)证明:
(I)证明: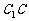 ⊥BD;
⊥BD;
(II)假定CD=2,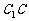 =
=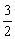 ,记面
,记面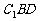 为
为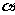 ,面CBD为
,面CBD为 ,求二面角
,求二面角 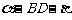 的平面角的余弦值;
的平面角的余弦值;
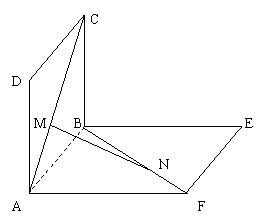 (III)当
(III)当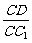 的值为多少时,能使
的值为多少时,能使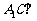 平面
平面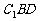 ?请给出证明。
?请给出证明。
2. (1997年全国高考)如图,在正方体
(1997年全国高考)如图,在正方体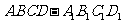 中,E,F分别是
中,E,F分别是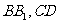 的中点.
的中点.
Ⅰ.证明AD⊥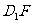 ;
;
Ⅱ.求AE与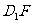 所成的角;
所成的角;
Ⅲ.证明面AED⊥面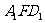 ;
;
Ⅳ.设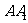 =2,求三棱锥
=2,求三棱锥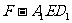 的体积
的体积
[答案与提示:1. (1)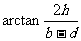 ;(3)
;(3)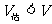 。 2. (2)90º; (4)
。 2. (2)90º; (4) =1。]
=1。]
1.(2002年北京高考)如图:在多面体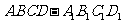 中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E、F两点,上下底面矩形的长、宽分别为
中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E、F两点,上下底面矩形的长、宽分别为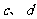 与
与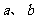 ,且
,且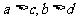 ,两底面间的距离为
,两底面间的距离为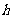 。
。
(1)求侧面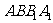 与底面
与底面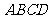 所成二面角的大小;
所成二面角的大小;
 (2)证明:
(2)证明: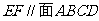
(3)在估测该多面体的体积时,经常运用近似公式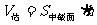 来计算。已知它的体积公式是
来计算。已知它的体积公式是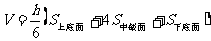 。
。
试判断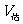 与
与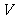 的大小关系,并加以证明。
的大小关系,并加以证明。
(注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面)
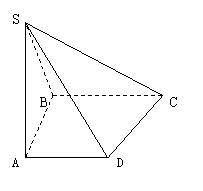
3.(2001年全国高考)如图:在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=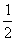 .
.
(1) 求四棱锥S-ABCD的体积;
(2) 求面SCD与面SBA所成的二面角的平面角的正切值.
[答案与提示:1.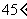 ;
;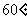 ;
;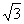 .
2.
.
2.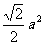 ;
;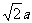 ;
;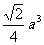 .
3.
.
3.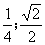 .
]
.
]
2.(1999年全国高考)如图,已知四棱柱ABCD-A'B'C'D',点E在棱D'D上,截面EAC∥D'B,且面EAC与底面ABCD所成的角为45°,AB=a
(1)求截面EAC的面积;
(2)求异面直线A'B'与AC之间的距离;
 (3)求三棱锥B'-EAC的体积.
(3)求三棱锥B'-EAC的体积.
1.(1998年全国高考)已知斜三棱柱ABC-A'B'C'的侧面A'ACC'与底面ABC垂直,∠ABC=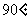 ,BC=2,AC=
,BC=2,AC=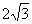 且AA'⊥A'C,AA'=A'C.
且AA'⊥A'C,AA'=A'C.
①求侧棱AA'与底面ABC所成角的大小;
②求侧面A'ABB'与底面ABC所成二面角的大小;
 ③求顶点C到侧面A'ABB'的距离.
③求顶点C到侧面A'ABB'的距离.
2.(2001年全国高考)已知复数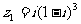 ,
,
(Ⅰ)求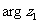 及
及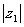 ;
;
(Ⅱ)当复数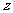 满足
满足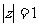 ,求
,求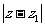 的最大值.
的最大值.
[答案与提示:1.当θ=arctan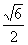 时,y取得最大值arctan
时,y取得最大值arctan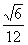 ; 2.(Ⅰ)
; 2.(Ⅰ)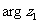 =
=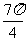 ,
,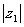 =
=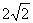 ;(Ⅱ)
;(Ⅱ)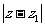 的最大值为
的最大值为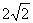 +1.]
+1.]
1.(1999年全国高考) 设复数z=3cosθ+2isinθ,求函数y=θ-argz(0<θ<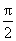 的最大值以及对应的θ值.
的最大值以及对应的θ值.
3.(1997年全国高考)已知复数z=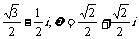 ,复数
,复数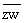 ,z2w3在复数平面上所对应的点分别为P,Q,证明△OPQ是等腰直角三角形(其中O是原点).
,z2w3在复数平面上所对应的点分别为P,Q,证明△OPQ是等腰直角三角形(其中O是原点).
[答案与提示:1.(Ⅰ)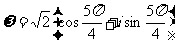 ;(Ⅱ)
;(Ⅱ)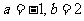 . 2.
. 2.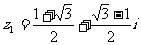 ;
;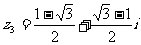 . 3.略.]
. 3.略.]
2.(1995年全国高考)在复平面上,一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O(O为原点),已知Z2对应复数z2=1+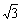 i,求点Z1和Z3所对应的复数.
i,求点Z1和Z3所对应的复数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com