(一)问题提出

1．点P(x0，y0)和圆锥曲线C：f(x，y)=0有哪几种位置关系？它们的条件是什么？

引导学生回答，点P与圆锥曲线C的位置关系有：点P在曲线C上、点P在曲线C内部(含焦点区域)、点P在曲线的外部(不含焦点的区域)．那么这三种位置关系的条件是什么呢？这是我们要分析的问题之一．

2．直线l：Ax+By+C=0和圆锥曲线C：f(x，y)=0有哪几种位置关系？

引导学生类比直线与圆的位置关系回答．直线l与圆锥曲线C的位置关系可分为：相交、相切、相离．那么这三种位置关系的条件是什么呢？这是我们要分析的问题之二．

3．疑点：直线与圆锥曲线位置关系的判定方法中△=0不是相切的充要条件．

(解决办法：用图形向学生讲清楚这一点．)

2．难点：圆锥曲线上存在关于直线对称的两点，求参数的取值范围．

(解决办法：利用判别式法和内点法进行讲解．)

1．重点：直线与圆锥曲线的相交的有关问题．

(解决办法：先引导学生归纳出直线与圆锥曲线的位置关系，再加以应用．)

(三)学科渗透点

通过点与圆锥曲线的位置及其判定，渗透归纳、推理、判断等方面的能力．

(二)能力训练点

通过对点、直线与圆锥曲线的位置关系的研究，培养学生综合运用直线、圆锥曲线的各方面知识的能力．

(一)知识教学点

使学生掌握点、直线与圆锥曲线的位置及其判定，重点掌握直线与圆锥曲线相交的有关问题．

9.熟练掌握两角和、差、倍、降幂公式及其逆向应用了吗？

　　 理解公式之间的联系：

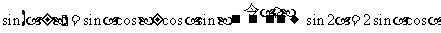
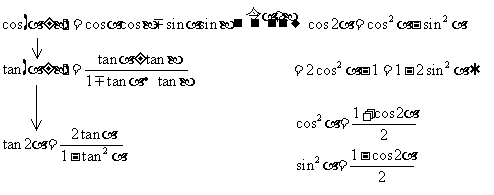
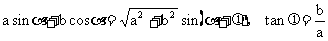
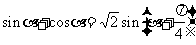
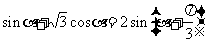
　　 应用以上公式对三角函数式化简。(化简要求：项数最少、函数种类最少，分母中不含三角函数，能求值，尽可能求值。)

　　 具体方法：

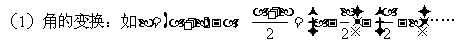
　　 (2)名的变换：化弦或化切

　　 (3)次数的变换：升、降幂公式

　　 (4)形的变换：统一函数形式，注意运用代数运算。

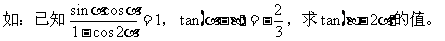
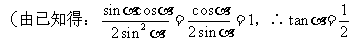
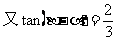
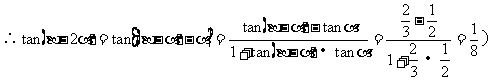
10 正、余弦定理的各种表达形式你还记得吗？如何实现边、角转化，而解斜三角形？

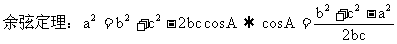
　　 (应用：已知两边一夹角求第三边；已知三边求角。)

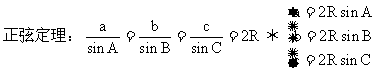
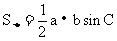
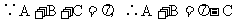
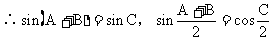
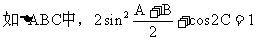
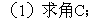
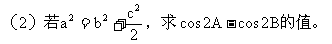
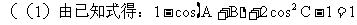
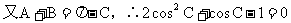
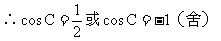
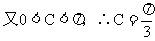
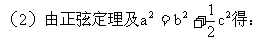
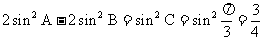
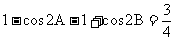
11用反三角函数表示角时要注意角的范围。

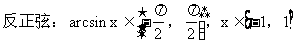
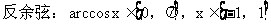
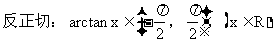
8.熟练掌握同角三角函数关系和诱导公式了吗？

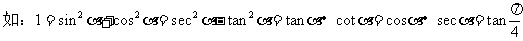
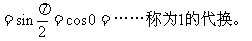
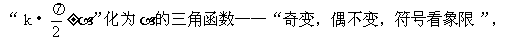
“奇”、“偶”指k取奇、偶数。

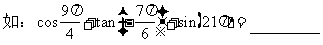
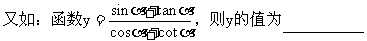
　　 A. 正值或负值　　　　　　 B. 负值　　　　 C. 非负值　　　　　　 D. 正值

7. 熟练掌握三角函数图象变换了吗？

　　 (平移变换、伸缩变换)

　　 平移公式：

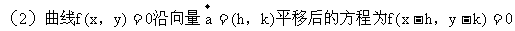
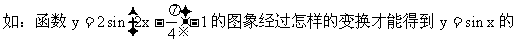
图象？