
4.在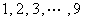 这
这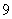 个自然数中,任取
个自然数中,任取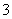 个不同的数.
个不同的数.
(1)求这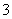 个数中至少有
个数中至少有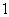 个是偶数的概率;
个是偶数的概率;
(2)求这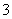 个数和为18的概率;
个数和为18的概率;
(3)设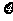 为这
为这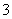 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为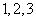 ,则有两组相邻的数
,则有两组相邻的数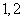 和
和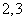 ,此时
,此时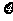 的值是
的值是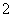 ).求随机变量
).求随机变量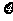 的分布列及其数学期望
的分布列及其数学期望 .
.
3.已知点F(0,1),点P在x轴上运动,M点在y轴上,N为动点,且满足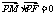 ,
,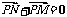 .
.
(1)求动点N的轨迹C方程;
(2)由直线y= -1上一点Q向曲线C引两条切线,切点分别为A,B,求证:AQ⊥BQ.
2.在极坐标系中,从极点O作直线与另一直线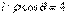 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使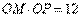 .
.
(1)求点P的轨迹方程;
(2)设R为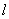 上任意一点,试求RP的最小值
上任意一点,试求RP的最小值
1.已知矩阵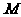
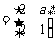 ,其中
,其中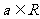 ,若点
,若点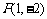 在矩阵
在矩阵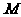 的变换下得到点
的变换下得到点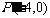 ,
,
(1)求实数a的值;
(2)求矩阵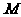 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
C.选修4-4:坐标系与参数方程
(总分40分,加试时间30分钟)
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内.解答过程应写在答题卷的相应位置上,在其它地方答题无效。
21.B.选修4-2:矩阵与变换
23.必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
已知函数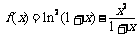 ,
,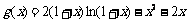 .
.
(1)证明:当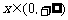 时,
时,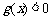 ;
;
(2)求函数 的的极值.
的的极值.
22. 必做题, 本小题10分.解答时应写出文字说明、证明过程或演算步骤.
如图,在三棱柱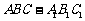 中,
中,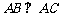 ,顶点
,顶点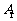 在底面
在底面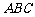 上的射影恰为点B,且
上的射影恰为点B,且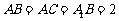 .
.
(1)求棱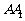 与BC所成的角的大小;
与BC所成的角的大小;
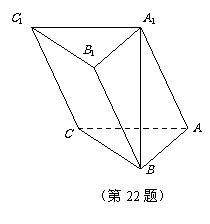 (2)在棱
(2)在棱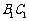 上确定一点P,使
上确定一点P,使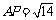 ,并求出二面角
,并求出二面角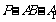 的平面角的余弦值.
的平面角的余弦值.
21.(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
 A.选修4-1 几何证明选讲
A.选修4-1 几何证明选讲
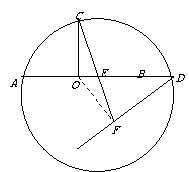
如图,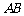 是⊙
是⊙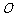 的直径,
的直径,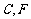 是⊙
是⊙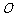 上的两点,
上的两点,
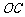 ⊥
⊥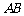 ,过点
,过点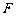 作⊙
作⊙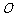 的切线FD交
的切线FD交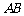 的延长
的延长
线于点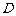 .连结
.连结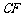 交
交
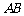 于点
于点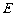 .
.
求证: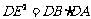 .
.
B.选修4-2 矩阵与变换
求矩阵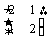 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C.选修4-4 坐标系与参数方程
已知曲线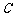 的极坐标方程是
的极坐标方程是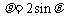 ,直线
,直线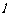 的参数方程是
的参数方程是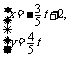 (
(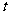 为参数).
为参数).
(1)将曲线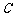 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线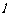 与
与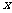 轴的交点是
轴的交点是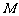 ,
,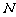 是曲线
是曲线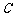 上一动点,求
上一动点,求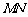 的最大值.
的最大值.
D.选修4-5 不等式选讲
设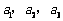 均为正数,且
均为正数,且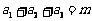 ,求证
,求证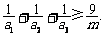
20.(本题满分16分)
已知函数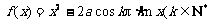 ,
,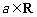 ,且
,且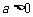 ).
).
(1)讨论函数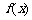 的单调性;
的单调性;
(2)若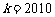 ,关于
,关于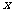 的方程
的方程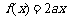 有唯一解,求a的值.
有唯一解,求a的值.
数学试卷 第4页(共4页)
19. (本题满分16分)
设数列{an}是由正数组成的等比数列,公比为q,Sn是其前n项和.
(1)证明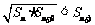 ;
;
(2)设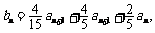 记数列
记数列 的前n项和为Tn,试比较q2Sn和Tn的大小.
的前n项和为Tn,试比较q2Sn和Tn的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com