
18.本题主要考查直线、圆、椭圆以及不等式等知识点,考查学生数形结合、函数与方程等思想的应用,以及学生分析问题与解决问题的能力.讲评时要强化解析几何的本质方法――解析法,从几何性质上分析,用代数的方法求解.第(1)小题求定点F坐标时强调分离参数的意识;第(2)小题判断r范围时也可联立方程组用代数法计算,在研究二元函数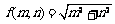 范围时,法一:消元,转化为一元函数求值域,此时要注意定义域的影响;法二:数形结合,转化为研究椭圆
范围时,法一:消元,转化为一元函数求值域,此时要注意定义域的影响;法二:数形结合,转化为研究椭圆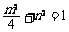 上动点到原点距离的范围.另外,
上动点到原点距离的范围.另外,
17.本题主要考查古典概率的计算及其相关知识,要求学生列举全面,书写规范.尤其注意此类问题的答题格式:设事件、说明概型、计算各基本事件种数、求值、作答.古典概率是必修3概率部分的中心内容,以列举法为主.本题结合列举法,留给学生能力发挥的空间,可以列举36种基本事件,如果看问题深刻一些,只要列举6种基本事件,理科学生还可以用排列知识求解.也可以与几何概型链接:
变题:田忌和齐王约定中午十二点到一点间到赛马场商定赛马事宜,求田忌在齐王前到但等候不超过一刻钟的概率.
16.本题主要考查线面平行、垂直的的判定和证明、锥体的体积公式等相关知识,考查空间想象能力.讲评时应强调立体几何中有关平行与垂直定理的符号语言表达,要求规范.
第(2)小题求四面体体积时要注意等积转化,培养学生的转化意识.
15.本题是向量与三角结合的题型.以向量为背景,考查了两角和与差的正余弦公式、余弦定理、向量的运算、面积公式、基本不等式等知识点,考查学生的公式、定理的选用能力(运算方向、运算途径的确定).第(1)小题要注意角的范围的判断;第(2)小题要注意等号成立的条件.
近三年江苏高考解答题均没有在三角形背景下考查三角向量,对三角、向量、解三角形等知识联系起来命题的形式值得关注.
14.考查数列、合情推理、三角函数的性质等相关内容,难题.采用特殊值法求出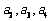 分别为
分别为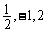 ,由不完全归纳法得出
,由不完全归纳法得出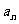 周期为3,再利用三角函数的图像与性质构造出
周期为3,再利用三角函数的图像与性质构造出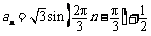 .答案不唯一,当
.答案不唯一,当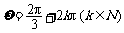 时,均可构造出相应的三角函数式;当
时,均可构造出相应的三角函数式;当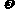 值取定后A、B、
值取定后A、B、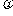 的值唯一确定
的值唯一确定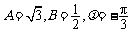 .
.
13.考查直线方程、线性规划等相关知识,考查运动与变化,对学生数形结合能力、函数方程、转化和化归的意识考查要求较高,较难题.点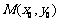 在直线
在直线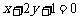 上,利用线性规划知识画出可行域为
上,利用线性规划知识画出可行域为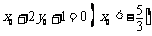 ,可行域区域内的点与原点连线的斜率范围是
,可行域区域内的点与原点连线的斜率范围是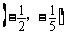 ,此题中正确画出可行域是前提,明白
,此题中正确画出可行域是前提,明白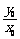 的几何意义是关键.
的几何意义是关键.
12.考查向量的数量积,中档题.讲评解决数量积问题的三种常用方法:法一:定义法,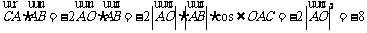 ;法二:建系设点进行坐标计 算;法三:向量转化,
;法二:建系设点进行坐标计 算;法三:向量转化,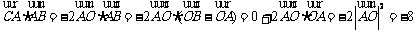 ;另外还可利用由一般到特殊的思想方法,把菱形特殊化为正方形,解法更为简洁.
;另外还可利用由一般到特殊的思想方法,把菱形特殊化为正方形,解法更为简洁.
11.考查等差数列的相关内容,中档题.法一:分类讨论,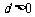 时,
时,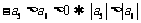 ;
;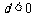 时,
时,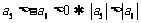 ;法二:
;法二: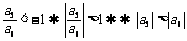 .
.
10.考查双曲线的几何性质,中档题.法一:首先判断出点(5, 0)为右焦点,因为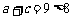 ,所以点P在双曲线右支上,再由双曲线定义得
,所以点P在双曲线右支上,再由双曲线定义得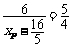 ,解得
,解得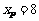 .法二:设
.法二:设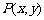 ,则
,则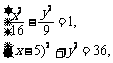 解得
解得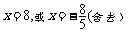 ,所以P(8,
,所以P(8,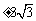 ).现在考纲中对双曲线、抛物线的要求比较低,对圆锥曲线的定义及基本量的运算要重视,可适当补充关于椭圆、双曲线、抛物线的相关问题
).现在考纲中对双曲线、抛物线的要求比较低,对圆锥曲线的定义及基本量的运算要重视,可适当补充关于椭圆、双曲线、抛物线的相关问题
9.考查三角函数的图像与性质及直线方程,考查学生的图形分析能力,中档题.先求出点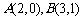 ,再求得直线方程为
,再求得直线方程为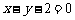 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com