
11.若曲线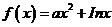 存在垂直于
存在垂直于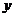 轴的切线,则实数
轴的切线,则实数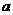 的取值范围是 .
的取值范围是 .
解析 解析 由题意该函数的定义域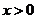 ,由
,由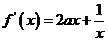 。因为存在垂直于
。因为存在垂直于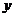 轴的切线,故此时斜率为
轴的切线,故此时斜率为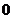 ,问题转化为
,问题转化为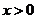 范围内导函数
范围内导函数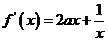 存在零点。
存在零点。
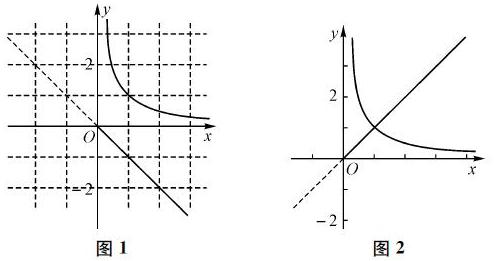
解法1 (图像法)再将之转化为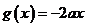 与
与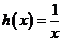 存在交点。当
存在交点。当 不符合题意,当
不符合题意,当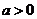 时,如图1,数形结合可得显然没有交点,当
时,如图1,数形结合可得显然没有交点,当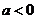 如图2,此时正好有一个交点,故有
如图2,此时正好有一个交点,故有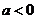 应填
应填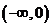
或是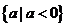 。
。
解法2 (分离变量法)上述也可等价于方程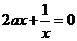 在
在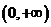 内有解,显然可得
内有解,显然可得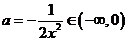
10.(2009辽宁卷文)若函数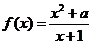 在
在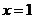 处取极值,则
处取极值,则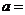
解析 f’(x)=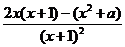
f’(1)=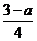 =0
Þ a=3
=0
Þ a=3
答案 3
9.(2009天津卷理)设函数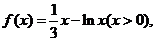 则
则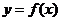 ( )
( )
A在区间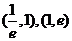 内均有零点。
内均有零点。
B在区间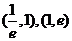 内均无零点。
内均无零点。
C在区间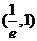 内有零点,在区间
内有零点,在区间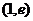 内无零点。
内无零点。
D在区间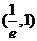 内无零点,在区间
内无零点,在区间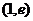 内有零点。
内有零点。
[考点定位]本小考查导数的应用,基础题。
解析 由题得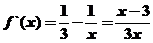 ,令
,令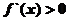 得
得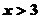 ;令
;令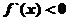 得
得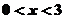 ;
;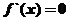 得
得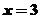 ,故知函数
,故知函数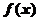 在区间
在区间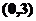 上为减函数,在区间
上为减函数,在区间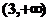
为增函数,在点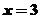 处有极小值
处有极小值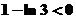 ;又
;又
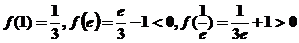 ,故选择D。
,故选择D。
8.(2009辽宁卷理)若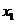 满足2x+
满足2x+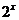 =5,
=5,
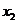 满足2x+2
满足2x+2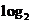 (x-1)=5,
(x-1)=5, 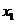 +
+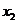 = ( )
= ( )
A.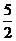 B.3 C.
B.3 C.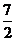 D.4
D.4
答案 C
解析 由题意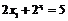 ①
①
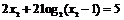 ②
②
所以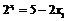 ,
,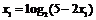
即2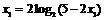
令2x1=7-2t,代入上式得7-2t=2log2(2t-2)=2+2log2(t-1)
∴5-2t=2log2(t-1)与②式比较得t=x2 于是2x1=7-2x2
7.(2009湖南卷文)若函数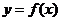 的导函数在区间
的导函数在区间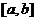 上是增函数,
上是增函数,
则函数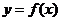 在区间
在区间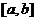 上的图象可能是 ( )
上的图象可能是 ( )
|
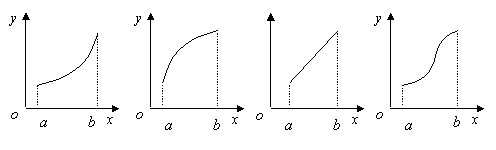

A . B. C. D.
解析 因为函数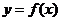 的导函数
的导函数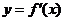 在区间
在区间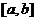 上是增函数,即在区间
上是增函数,即在区间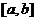 上各点处的斜率
上各点处的斜率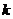 是递增的,由图易知选A. 注意C中
是递增的,由图易知选A. 注意C中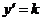 为常数噢.
为常数噢.
6.(2009全国卷Ⅱ理)曲线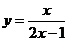 在点
在点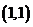 处的切线方程为 ( )
处的切线方程为 ( )
A. 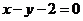 B.
B. 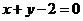 C.
C.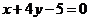 D.
D. 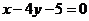
答案 B
解 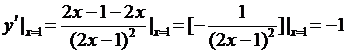 ,
,
故切线方程为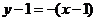 ,即
,即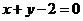 故选B.
故选B.
5.(2009江西卷理)设函数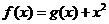 ,曲线
,曲线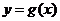 在点
在点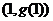 处的切线方程为
处的切线方程为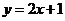 ,则曲线
,则曲线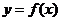 在点
在点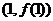 处切线的斜率为 ( )
处切线的斜率为 ( )
A.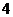 B.
B.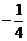 C.
C.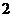 D.
D.
答案 A
解析 由已知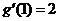 ,而
,而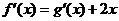 ,所以
,所以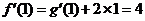 故选A
故选A
力。
4.(2009江西卷文)若存在过点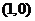 的直线与曲线
的直线与曲线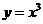 和
和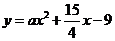 都相切,则
都相切,则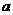 等于 ( )
等于 ( )
A.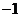 或
或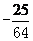 B.
B.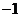 或
或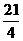 C.
C.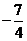 或
或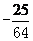 D.
D.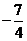 或
或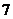
答案 A
解析 设过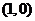 的直线与
的直线与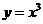 相切于点
相切于点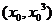 ,所以切线方程为
,所以切线方程为
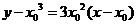
即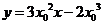 ,又
,又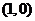 在切线上,则
在切线上,则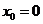 或
或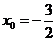 ,
,
当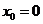 时,由
时,由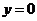 与
与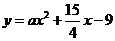 相切可得
相切可得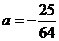 ,
,
当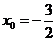 时,由
时,由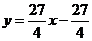 与
与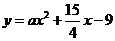 相切可得
相切可得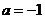 ,所以选
,所以选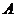 .
.
3.(2009安徽卷理)已知函数 在R上满足
在R上满足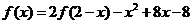 ,则曲线
,则曲线
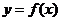 在点
在点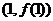 处的切线方程是 ( )
处的切线方程是 ( )
A.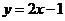 B.
B.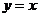 C.
C.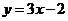 D.
D.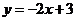
答案 A
解析 由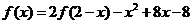 得几何
得几何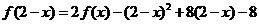 ,
,
即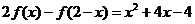 ,∴
,∴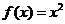 ∴
∴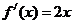 ,∴切线方程
,∴切线方程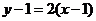 ,即
,即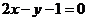 选A
选A
2.(2009全国卷Ⅰ理) 已知直线y=x+1与曲线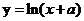 相切,则α的值为( )
相切,则α的值为( )
A.1 B. 2 C.-1 D.-2
答案 B
解:设切点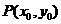 ,则
,则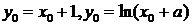 ,又
,又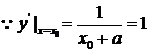
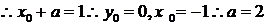 .故答案 选B
.故答案 选B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com