
4.(2009浙江文)已知椭圆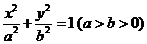 的左焦点为
的左焦点为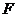 ,右顶点为
,右顶点为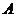 ,点
,点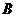 在椭圆上,且
在椭圆上,且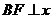 轴, 直线
轴, 直线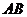 交
交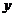 轴于点
轴于点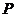 .若
.若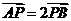 ,则椭圆的离心率是( )
,则椭圆的离心率是( )


A.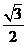 B.
B.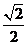 C.
C.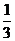 D.
D.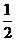
[解析]对于椭圆,因为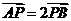 ,则
,则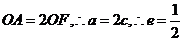
 [答案]D
[答案]D
3.(2009浙江理)过双曲线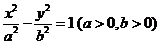 的右顶点
的右顶点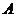 作斜率为
作斜率为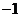 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为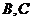 .若
.若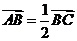 ,则双曲线的离心率是
( )
,则双曲线的离心率是
( ) 

A.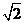 B.
B.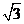 C.
C.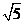 D.
D.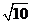
[解析]对于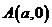 ,则直线方程为
,则直线方程为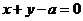 ,直线与两渐近线的交点为B,C,
,直线与两渐近线的交点为B,C,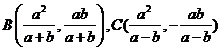 则有
则有
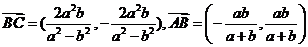 ,因
,因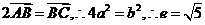 .
.
[答案]C
2.(2009全国卷Ⅰ理)已知椭圆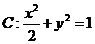 的右焦点为
的右焦点为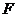 ,右准线为
,右准线为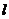 ,点
,点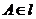 ,线段
,线段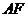 交
交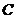 于点
于点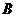 ,若
,若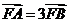 ,则
,则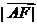 =( )
=( )
A. 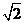 B.
2 C.
B.
2 C.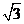 D. 3
D. 3


[解析]过点B作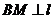 于M,并设右准线
于M,并设右准线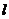 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意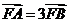 ,故
,故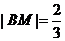 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得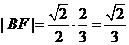
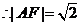 .故选A
.故选A 

[答案]A
1.(2009全国卷Ⅰ理)设双曲线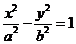 (a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于( )
(a>0,b>0)的渐近线与抛物线y=x2 +1相切,则该双曲线的离心率等于( )
A.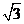 B.2 C.
B.2 C.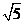 D.
D.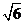


[解析]设切点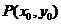 ,则切线的斜率为
,则切线的斜率为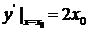 .
.
由题意有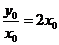 又
又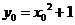
解得: 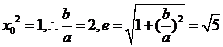 .
. 

[答案]C
2009年高考题
2009年高考数学试题分类汇编--圆锥曲线
17.(2007北京四中模拟一)在△ABC中,A点的坐标为(3,0),BC边长为2,且BC在y轴上的区间[-3,3]上滑动.
(1)求△ABC外心的轨迹方程;
(2)设直线l∶y=3x+b与(1)的轨迹交于E,F两点,原点到直线l的距离为d,求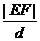 的最大值.并求出此时b的值.
的最大值.并求出此时b的值.
解 (1)设B点的坐标为(0,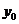 ),则C点坐标为(0,
),则C点坐标为(0,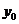 +2)(-3≤
+2)(-3≤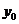 ≤1),
≤1),
则BC边的垂直平分线为y=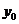 +1 ①
+1 ①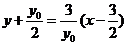 ②由①②消去
②由①②消去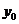 ,得
,得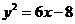 .∵
.∵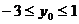 ,∴
,∴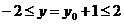 .故所求的△ABC外心的轨迹方程为:
.故所求的△ABC外心的轨迹方程为: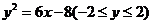 .
.
(2)将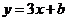 代入
代入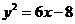 得
得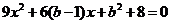 .由
.由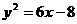 及
及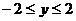 ,得
,得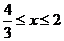 .所以方程①在区间
.所以方程①在区间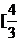 ,2
,2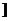 有两个实根.设
有两个实根.设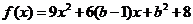 ,则方程③在
,则方程③在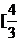 ,2
,2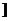 上有两个不等实根的充要条件是:
上有两个不等实根的充要条件是:
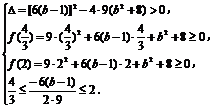 得
得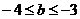
∵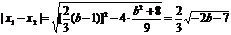 ∴
∴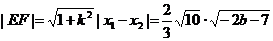
又原点到直线l的距离为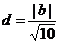 ,
,
∴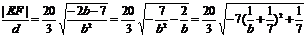 ∵
∵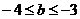 ,∴
,∴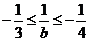 .
.
∴当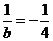 ,即
,即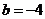 时,
时,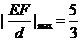 .
.
16. (江苏省泰兴市2007-2008学年第一学期高三调研)已知过点A(0,1),且方向向量为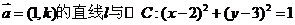 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数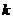 的取值范围;
的取值范围;
(2)求证: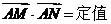 ;
;
(3)若O为坐标原点,且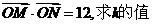 .
.
解 (1)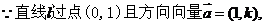

由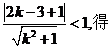
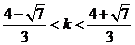 .
.
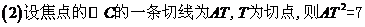
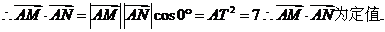
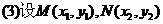

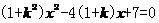
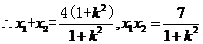
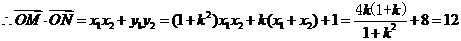
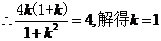
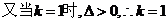 .
.
15.(广东地区2008年01月期末试题) 已知点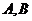 的坐标分别是
的坐标分别是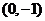 ,
,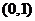 ,直线
,直线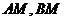 相交于点M,且它们的斜率之积为
相交于点M,且它们的斜率之积为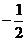 .
.
(1)求点M轨迹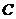 的方程;
的方程;
(2)若过点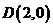 的直线
的直线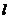 与(1)中的轨迹
与(1)中的轨迹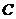 交于不同的两点
交于不同的两点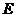 、
、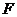 (
(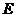 在
在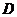 、
、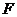 之间),试求
之间),试求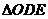 与
与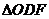 面积之比的取值范围(
面积之比的取值范围(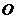 为坐标原点).
为坐标原点).
解(1)设点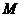 的坐标为
的坐标为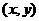 ,
,
∵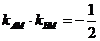 ,∴
,∴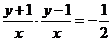 .
.
整理,得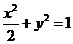 (
(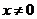 ),这就是动点M的轨迹方程.
),这就是动点M的轨迹方程.
(2)方法一 由题意知直线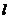 的斜率存在,
的斜率存在,
设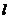 的方程为
的方程为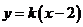 (
(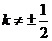 )
①
)
①
将①代入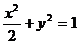 ,
,
得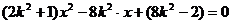 ,
,
由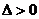 ,解得
,解得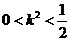 .
.
设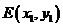 ,
,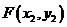 ,则
,则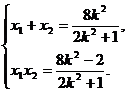 ②
②
令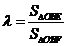 ,则
,则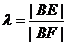 ,即
,即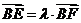 ,即
,即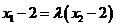 ,且
,且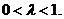
由②得,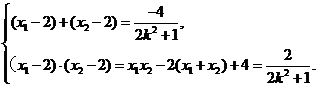
即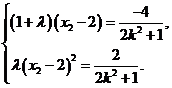
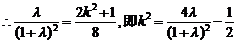 .
.
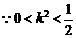 且
且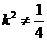
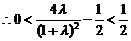 且
且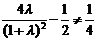 .
.
解得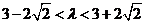 且
且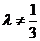
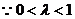 ,
,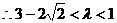 且
且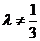 .
.
∴△OBE与△OBF面积之比的取值范围是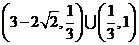 .
.
方法二 由题意知直线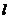 的斜率存在,
的斜率存在,
设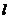 的方程为
的方程为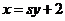
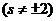 ①
①
将①代入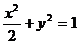 ,
,
整理,得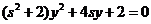 ,
,
由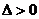 ,解得
,解得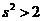 .
.
设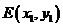 ,
,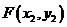 ,则
,则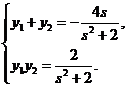 ②
②
令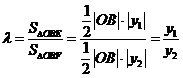 ,且
,且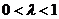 .
.
将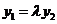 代入②,得
代入②,得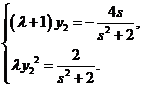
∴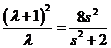 .即
.即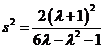 .
.
∵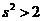 且
且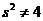 ,∴
,∴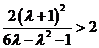 且
且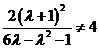 .
.
即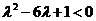 且
且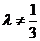 .
.
解得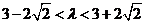 且
且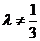 .
.
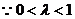 ,
,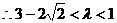 且
且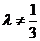 .
.
故△OBE与△OBF面积之比的取值范围是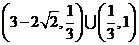 .
.
14.(江苏省南京市2008届高三第一次调研测试)已知:以点C (t, )(t∈R , t ≠ 0)为圆心的圆与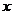 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
解 (1)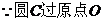 ,
,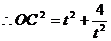 .
.
设圆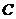 的方程是
的方程是 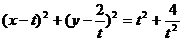
令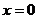 ,得
,得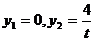 ;令
;令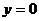 ,得
,得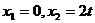
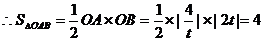 ,即:
,即: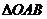 的面积为定值.
的面积为定值.
(2)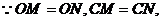
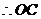 垂直平分线段
垂直平分线段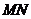 .
.
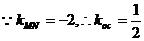 ,
,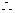 直线
直线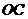 的方程是
的方程是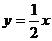 .
.
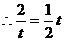 ,解得:
,解得: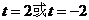
当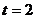 时,圆心
时,圆心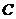 的坐标为
的坐标为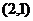 ,
,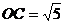 ,
,
此时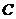 到直线
到直线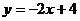 的距离
的距离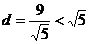 ,
,
圆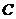 与直线
与直线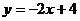 相交于两点.
相交于两点.
当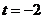 时,圆心
时,圆心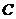 的坐标为
的坐标为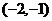 ,
,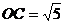 ,
,
此时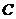 到直线
到直线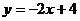 的距离
的距离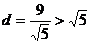
圆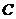 与直线
与直线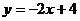 不相交,
不相交,
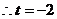 不符合题意舍去.
不符合题意舍去.
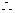 圆
圆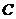 的方程为
的方程为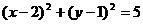 .
.
13.(唐山二模)⊙M:x2+y2=4,点P(x0,y0)在圆外,则直线x0x+y0y=4与⊙M的位置关系是_____
答案 相交
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com