
32.(2009湖南卷文)对于数列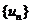 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的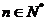 ,恒有
,恒有
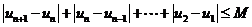 ,
, 
 则称数列
则称数列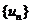 为
为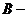 数列.
数列.
(Ⅰ)首项为1,公比为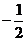 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;
(Ⅱ)设 是数列
是数列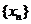 的前n项和.给出下列两组判断:
的前n项和.给出下列两组判断:
A组:①数列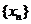 是B-数列, ②数列
是B-数列, ②数列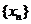 不是B-数列;
不是B-数列;
B组:③数列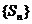 是B-数列, ④数列
是B-数列, ④数列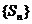 不是B-数列.
不是B-数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题.
判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列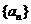 是B-数列,证明:数列
是B-数列,证明:数列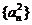 也是B-数列。
也是B-数列。
解: (Ⅰ)设满足题设的等比数列为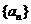 ,则
,则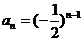 .于是
.于是
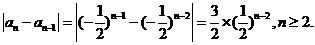
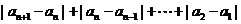


=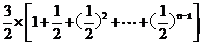 =
=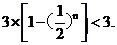
所以首项为1,公比为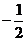 的等比数列是B-数列 .
的等比数列是B-数列 .
(Ⅱ)命题1:若数列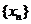 是B-数列,则数列
是B-数列,则数列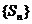 是B-数列.此命题为假命题.
是B-数列.此命题为假命题.
事实上设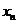 =1,
=1,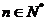 ,易知数列
,易知数列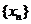 是B-数列,但
是B-数列,但 =n,
=n,
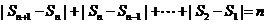 .
.
由n的任意性知,数列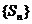 不是B-数列。
不是B-数列。
命题2:若数列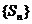 是B-数列,则数列
是B-数列,则数列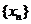 不是B-数列。此命题为真命题。
不是B-数列。此命题为真命题。
事实上,因为数列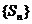 是B-数列,所以存在正数M,对任意的
是B-数列,所以存在正数M,对任意的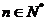 ,有
,有
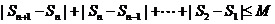 ,
,
即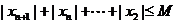 .于是
.于是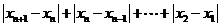
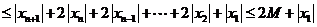 ,
,
所以数列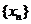 是B-数列。
是B-数列。
(注:按题中要求组成其它命题解答时,仿上述解法) 

(Ⅲ)若数列 是B-数列,则存在正数M,对任意的
是B-数列,则存在正数M,对任意的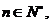 有
有
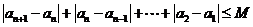 .
.
因为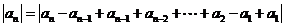
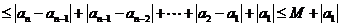 .
.
记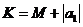 ,则有
,则有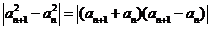
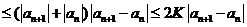 .
.
因此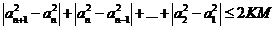 .
.
故数列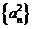 是B-数列.
是B-数列.
31.(2009四川卷文)设数列 的前
的前 项和为
项和为 ,对任意的正整数
,对任意的正整数 ,都有
,都有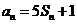 成立,记
成立,记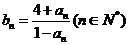 。
。


(I)求数列 与数列
与数列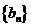 的通项公式;
的通项公式;
(II)设数列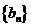 的前
的前 项和为
项和为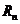 ,是否存在正整数
,是否存在正整数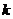 ,使得
,使得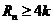 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数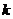 ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记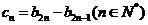 ,设数列
,设数列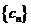 的前
的前 项和为
项和为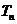 ,求证:对任意正整数
,求证:对任意正整数 都有
都有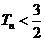 ;
;
解(I)当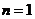 时,
时,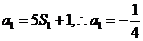


又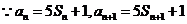
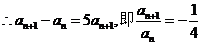
∴数列 是首项为
是首项为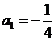 ,公比为
,公比为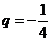 的等比数列,
的等比数列,
∴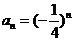 ,
,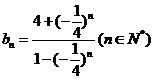 …………………………………3分
…………………………………3分
(II)不存在正整数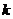 ,使得
,使得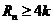 成立。
成立。
证明:由(I)知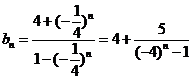


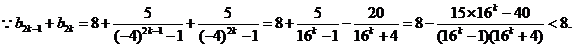
∴当n为偶数时,设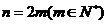


∴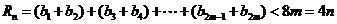
当n为奇数时,设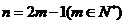
∴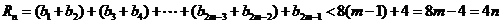
∴对于一切的正整数n,都有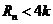


∴不存在正整数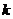 ,使得
,使得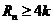 成立。
…………………………………8分
成立。
…………………………………8分
(III)由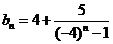 得
得


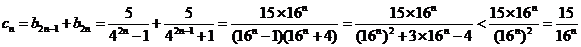 又
又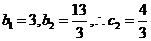 ,
,


当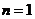 时,
时,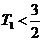 ,
,
当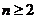 时,
时,
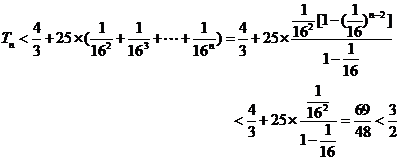
30.
(2009湖北卷理)已知数列 的前n项和
的前n项和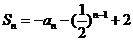 (n为正整数)。
(n为正整数)。
(Ⅰ)令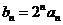 ,求证数列
,求证数列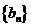 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)令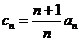 ,
,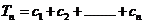 试比较
试比较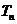 与
与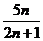 的大小,并予以证明。
的大小,并予以证明。
解(I)在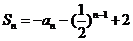 中,令n=1,可得
中,令n=1,可得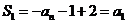 ,即
,即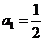
当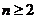 时,
时,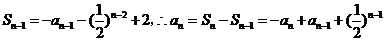 ,
,

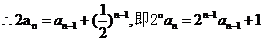 .
.
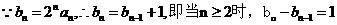 .
. 



又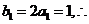 数列
数列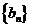 是首项和公差均为1的等差数列.
是首项和公差均为1的等差数列.
于是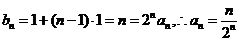 .
.
(II)由(I)得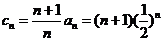 ,所以
,所以
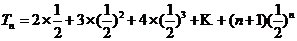
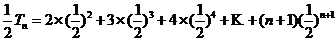
由①-②得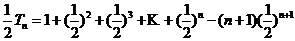


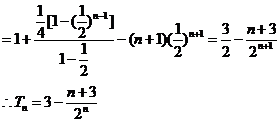
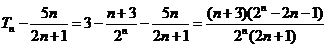
于是确定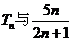 的大小关系等价于比较
的大小关系等价于比较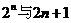 的大小
的大小
由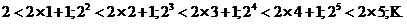


可猜想当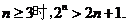 证明如下:
证明如下:
证法1:(1)当n=3时,由上验算显示成立。
(2)假设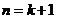 时
时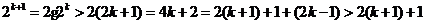
所以当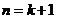 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切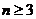 的正整数,都有
的正整数,都有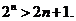
证法2:当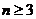 时
时
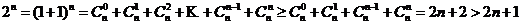
综上所述,当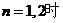
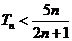 ,当
,当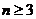 时
时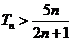
29.(2009江西卷理)各项均为正数的数列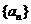 ,
,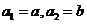 ,且对满足
,且对满足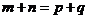 的正整数
的正整数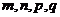 都有
都有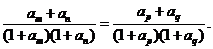
(1)当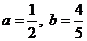 时,求通项
时,求通项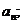


(2)证明:对任意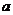 ,存在与
,存在与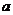 有关的常数
有关的常数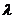 ,使得对于每个正整数
,使得对于每个正整数 ,都有
,都有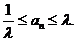
解:(1)由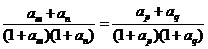 得
得
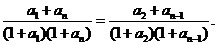 将
将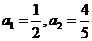 代入化简得
代入化简得 

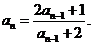
所以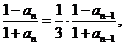


故数列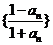 为等比数列,从而
为等比数列,从而
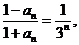 即
即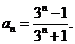
可验证,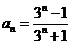 满足题设条件.
满足题设条件.
(2)
由题设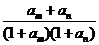 的值仅与
的值仅与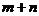 有关,记为
有关,记为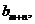 则
则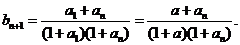


考察函数 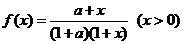 ,则在定义域上有
,则在定义域上有 

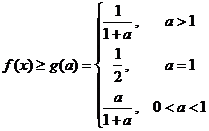
故对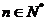 ,
,
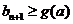 恒成立.
恒成立. 

又 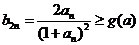 ,
,
注意到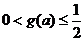 ,解上式得
,解上式得
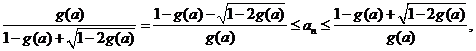
取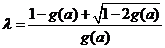 ,即有
,即有
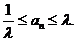 .
. 

27.(2009广东卷理)知曲线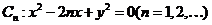 .从点
.从点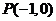 向曲线
向曲线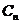 引斜率为
引斜率为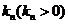 的切线
的切线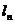 ,切点为
,切点为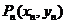 .
.
(1)求数列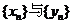 的通项公式;
的通项公式;
(2)证明: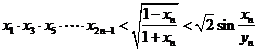 .
.
解:(1)设直线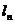 :
: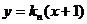 ,联立
,联立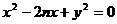 得
得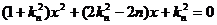 ,则
,则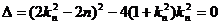 ,∴
,∴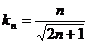 (
(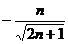 舍去)
舍去) 

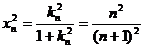 ,即
,即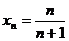 ,∴
,∴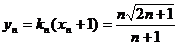
(2)证明:∵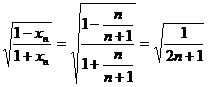


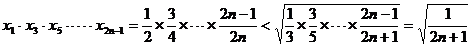
∴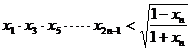
由于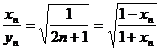 ,可令函数
,可令函数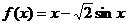 ,则
,则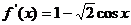 ,令
,令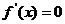 ,得
,得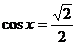 ,给定区间
,给定区间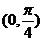 ,则有
,则有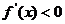 ,则函数
,则函数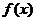 在
在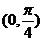 上单调递减,∴
上单调递减,∴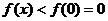 ,即
,即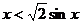 在
在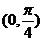 恒成立,又
恒成立,又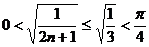 ,
,
则有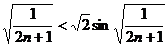 ,即
,即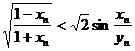 .
. 



28(2009安徽卷理)首项为正数的数列 满足
满足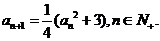


(I)证明:若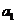 为奇数,则对一切
为奇数,则对一切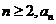 都是奇数;
都是奇数;
(II)若对一切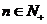 都有
都有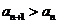 ,求
,求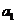 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知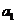 是奇数,假设
是奇数,假设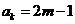 是奇数,其中
是奇数,其中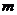 为正整数,
为正整数,
则由递推关系得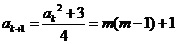 是奇数。
是奇数。


根据数学归纳法,对任何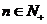 ,
,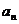 都是奇数。
都是奇数。
(II)(方法一)由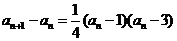 知,
知,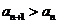 当且仅当
当且仅当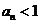 或
或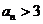 。
。
另一方面,若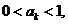 则
则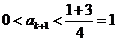 ;若
;若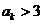 ,则
,则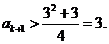
根据数学归纳法,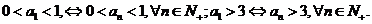
综合所述,对一切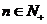 都有
都有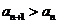 的充要条件是
的充要条件是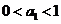 或
或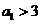 。
。
(方法二)由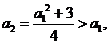 得
得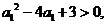 于是
于是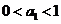 或
或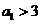 。
。
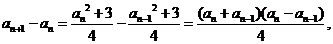


因为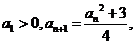 所以所有的
所以所有的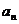 均大于0,因此
均大于0,因此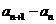 与
与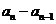 同号。
同号。
根据数学归纳法,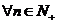 ,
,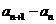 与
与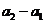 同号。
同号。


因此,对一切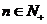 都有
都有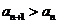 的充要条件是
的充要条件是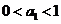 或
或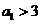 。
。
26.(2009山东卷理)等比数列{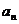 }的前n项和为
}的前n项和为 ,
已知对任意的
,
已知对任意的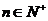 ,点
,点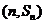 ,均在函数
,均在函数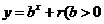 且
且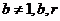 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(11)当b=2时,记 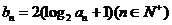


证明:对任意的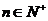 ,不等式
,不等式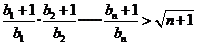 成立
成立
解:因为对任意的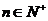 ,点
,点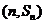 ,均在函数
,均在函数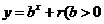 且
且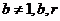 均为常数的图像上.所以得
均为常数的图像上.所以得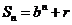 ,当
,当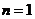 时,
时,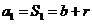 ,当
,当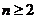 时,
时,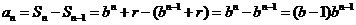 ,又因为{
,又因为{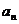 }为等比数列,所以
}为等比数列,所以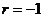 ,公比为
,公比为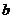 ,
,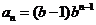
(2)当b=2时,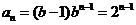 ,
, 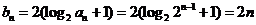
则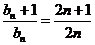 ,所以
,所以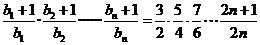


下面用数学归纳法证明不等式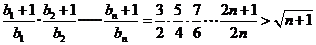 成立.
成立.
①
当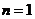 时,左边=
时,左边=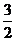 ,右边=
,右边=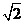 ,因为
,因为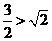 ,所以不等式成立.
,所以不等式成立.
②
假设当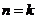 时不等式成立,即
时不等式成立,即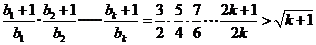 成立.则当
成立.则当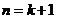 时,左边=
时,左边=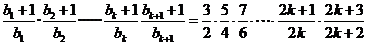
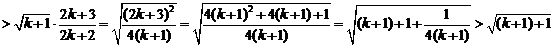
所以当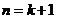 时,不等式也成立.
时,不等式也成立. 

由①、②可得不等式恒成立.
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知 求
求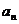 的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
的基本题型,并运用数学归纳法证明与自然数有关的命题,以及放缩法证明不等式.
24.(2009江苏卷)设 是公差不为零的等差数列,
是公差不为零的等差数列, 为其前
为其前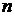 项和,满足
项和,满足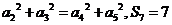 。
。
(1)求数列 的通项公式及前
的通项公式及前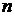 项和
项和 ;
;

(2)试求所有的正整数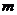 ,使得
,使得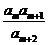 为数列
为数列 中的项。
中的项。

[解析] 本小题主要考查等差数列的通项、求和的有关知识,考查运算和求解的能力。满分14分。
(1)设公差为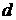 ,则
,则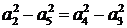 ,由性质得
,由性质得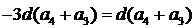 ,因为
,因为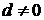 ,所以
,所以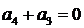 ,即
,即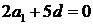 ,又由
,又由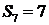 得
得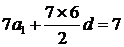 ,解得
,解得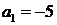 ,
,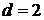 ,
,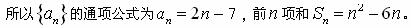
(2) (方法一)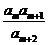 =
=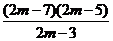 ,设
,设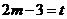 ,
,

则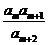 =
=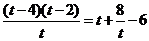 , 所以
, 所以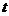 为8的约数
为8的约数

(方法二)因为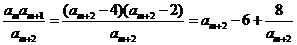 为数列
为数列 中的项,
中的项,
故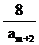 为整数,又由(1)知:
为整数,又由(1)知: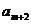 为奇数,所以
为奇数,所以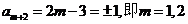
经检验,符合题意的正整数只有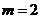 。
。 

25(2009江苏卷)对于正整数 ≥2,用
≥2,用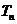 表示关于
表示关于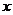 的一元二次方程
的一元二次方程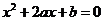 有实数根的有序数组
有实数根的有序数组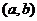 的组数,其中
的组数,其中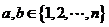 (
(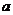 和
和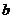 可以相等);对于随机选取的
可以相等);对于随机选取的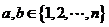 (
(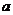 和
和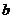 可以相等),记
可以相等),记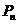 为关于
为关于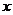 的一元二次方程
的一元二次方程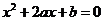 有实数根的概率。
有实数根的概率。
(1)求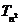 和
和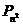 ;
;
(2)求证:对任意正整数 ≥2,有
≥2,有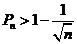 .
.
[解析] [必做题]本小题主要考查概率的基本知识和记数原理,考查探究能力。满分10分。



23.(2009北京理)已知数集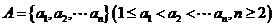 具有性质
具有性质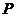 ;对任意的
;对任意的
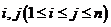 ,
,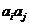 与
与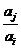 两数中至少有一个属于
两数中至少有一个属于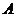 .
.
(Ⅰ)分别判断数集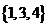 与
与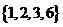 是否具有性质
是否具有性质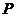 ,并说明理由;
,并说明理由;
(Ⅱ)证明: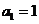 ,且
,且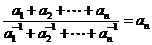 ;
;
(Ⅲ)证明:当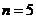 时,
时,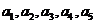 成等比数列.
成等比数列.
[解析]本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
(Ⅰ)由于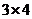 与
与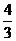 均不属于数集
均不属于数集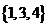 ,∴该数集不具有性质P.
,∴该数集不具有性质P.
由于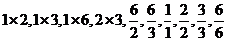 都属于数集
都属于数集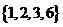 ,
,
∴该数集具有性质P.
(Ⅱ)∵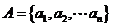 具有性质P,∴
具有性质P,∴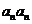 与
与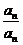 中至少有一个属于A,
中至少有一个属于A,
由于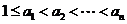 ,∴
,∴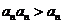 ,故
,故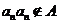 .
. 

从而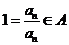 ,∴
,∴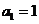 .
.
∵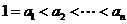 ,
∴
,
∴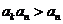 ,故
,故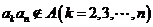 .
.
由A具有性质P可知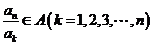 .
.
又∵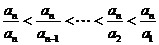 ,
,
∴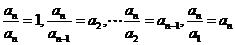 ,
,
从而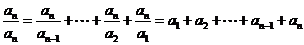 ,
,
∴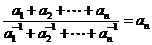 .
. 

(Ⅲ)由(Ⅱ)知,当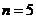 时,有
时,有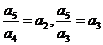 ,即
,即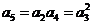 ,
,
∵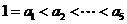 ,∴
,∴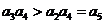 ,∴
,∴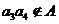 ,
,
由A具有性质P可知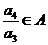 .
.
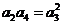 ,得
,得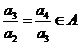 ,且
,且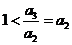 ,∴
,∴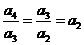 ,
,
∴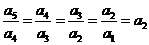 ,即
,即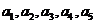 是首项为1,公比为
是首项为1,公比为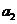 成等比数列..k.s.5.
成等比数列..k.s.5.
22.(2009全国卷Ⅰ理)在数列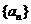 中,
中,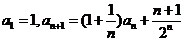
(I)设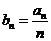 ,求数列
,求数列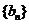 的通项公式
的通项公式
(II)求数列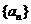 的前
的前 项和
项和
分析:(I)由已知有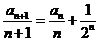
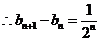
利用累差迭加即可求出数列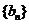 的通项公式:
的通项公式: 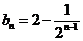 (
(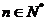 )
)
(II)由(I)知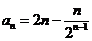 ,
,
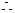
 =
=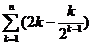
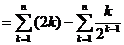
而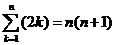 ,又
,又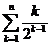 是一个典型的错位相减法模型,
是一个典型的错位相减法模型,
易得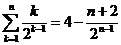
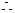
 =
=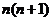
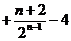
评析:09年高考理科数学全国(一)试题将数列题前置,考查构造新数列和利用错位相减法求前n项和,一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
21.(2009年广东卷文)(本小题满分14分)
已知点(1,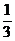 )是函数
)是函数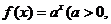 且
且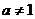 )的图象上一点,等比数列
)的图象上一点,等比数列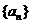 的前
的前 项和为
项和为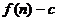 ,数列
,数列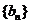
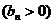 的首项为
的首项为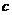 ,且前
,且前 项和
项和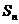 满足
满足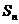 -
-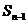 =
=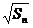 +
+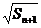 (
(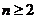 ).
).
(1)求数列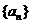 和
和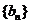 的通项公式;
的通项公式;
(2)若数列{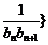 前
前 项和为
项和为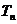 ,问
,问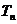 >
>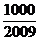 的最小正整数
的最小正整数 是多少?
是多少? 

解(1)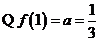 ,
,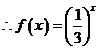
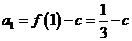 ,
,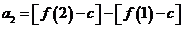
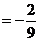 ,
,
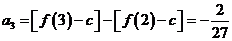 .
.
又数列 成等比数列,
成等比数列,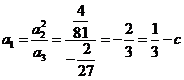 ,所以
,所以 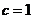 ;
;
又公比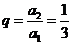 ,所以
,所以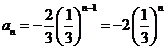
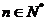 ;
;
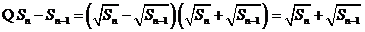
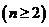
又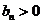 ,
,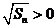 ,
,
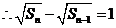 ;
;
数列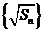 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,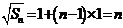 ,
, 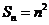
当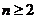 ,
,
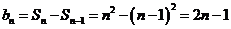 ;
;
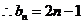 (
(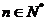 );
);
(2)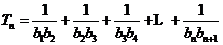
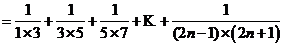
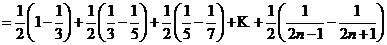
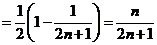 ;
;
由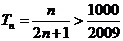 得
得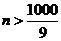 ,满足
,满足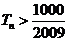 的最小正整数为112.
的最小正整数为112.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com