
3.(本小题满分12分)
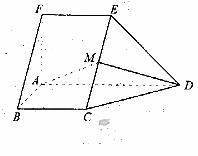 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 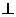 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB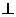 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=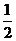 AD
AD 

(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD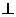 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。 

如图所示,建立空间直角坐标系,
点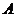 为坐标原点。设
为坐标原点。设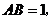 依题意得
依题意得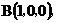
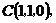
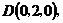
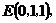
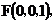
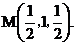
(I)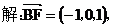
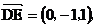


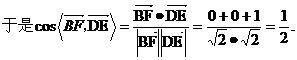
所以异面直线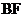 与
与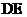 所成的角的大小为
所成的角的大小为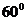 .
.
(II)证明: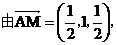
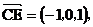
 ,
,
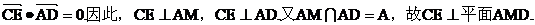
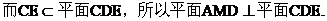


(III)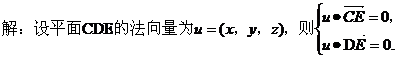
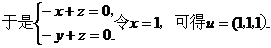
又由题设,平面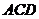 的一个法向量为
的一个法向量为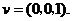
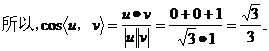


|
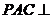 平面
平面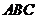 ,
,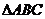
是以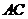 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,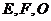 分别为
分别为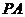 ,
,
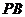 ,
,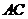 的中点,
的中点,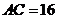 ,
,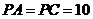 .
.
(I)设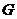 是
是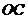 的中点,证明:
的中点,证明: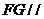 平面
平面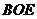 ;
;
(II)证明:在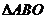 内存在一点
内存在一点 ,使
,使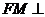 平面
平面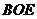 ,并求点
,并求点 到
到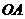 ,
,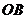 的距离.
的距离.
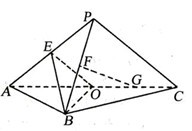
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为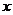 轴,
轴,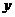 轴,
轴,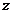 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O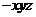 ,
,


则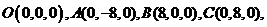
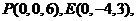
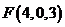 ,由题意得,
,由题意得,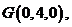 因
因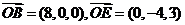 ,因此平面BOE的法向量为
,因此平面BOE的法向量为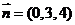 ,
,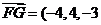 得
得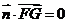 ,又直线
,又直线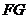 不在平面
不在平面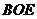 内,因此有
内,因此有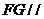 平面
平面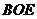
2.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________。
[解析]设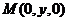 由
由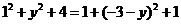 可得
可得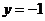 故
故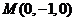
[答案](0,-1,0) 

1.若等边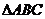 的边长为
的边长为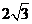 ,平面内一点
,平面内一点 满足
满足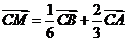 ,则
,则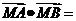 _________
_________ 

6.(江西省鹰潭市2008届高三第一次模拟) 三棱锥P-ABC的侧棱PA、PB、PC两两垂直,侧面面积分别是6,4,3,则三棱锥的体积是 ( )
A. 4 B. 6 C. 8 D. 10
答案 A
5.(吉林省吉林市2008届上期末)设正方体的棱长为,则它的外接球的表面积为( )
A.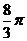 B.2π C.4π D.
B.2π C.4π D.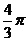
答案C
4.(湖北省黄冈中学2008届高三第一次模拟考试)已知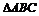 中,AB=2,BC=1,
中,AB=2,BC=1,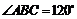 ,平面ABC外一点P满足PA=PB=PC=2,则三棱锥P-ABC的体积是( )
,平面ABC外一点P满足PA=PB=PC=2,则三棱锥P-ABC的体积是( )
A.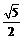 B.
B.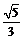 C.
C.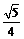 D.
D.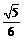
答案 D
3. (福建省南靖一中2008年第四次月考) 球面上有三点A、B、C,任意两点之间的球面距离
都等于球大圆周长的四分之一,且过这三点的截面圆的面积为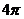 ,则此球的体积为
,则此球的体积为
( )
A. 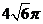 B.
B. 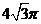 C.
C. 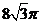 D.
D. 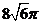
答案 D
2.(2008江苏省启东中学高三综合测试四)一个与球心距离为1的平面截球体所得的圆面面积为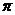 ,则球的体积为
( )
,则球的体积为
( )
A. 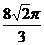 B.
B. 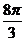 C.
C. 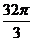 D. 8
D. 8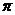
答案 A
1.(2008江苏省启东中学高三综合测试二)如图在正三棱锥A-BCD中,
E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD
的体积是 ( )

答案 B
4. (2009闸北区) 如图,在四棱锥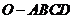 中,底面
中,底面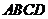 是边长为2的正方形,
是边长为2的正方形,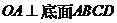 ,
,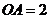 ,
,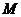 为
为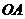 的中点.
的中点.
 (Ⅰ)求四棱锥
(Ⅰ)求四棱锥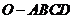 的体积;
的体积;
(Ⅱ)求异面直线OB与MD所成角的大小.
解:(Ⅰ)由已知可求得,正方形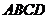 的面积
的面积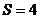 ,……………………………2分
,……………………………2分
所以,求棱锥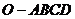 的体积
的体积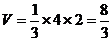 ………………………………………4分
………………………………………4分
(Ⅱ)方法一(综合法)
设线段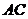 的中点为
的中点为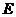 ,连接
,连接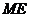 ,
,
则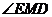 为异面直线OC与
为异面直线OC与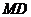 所成的角(或其补角) ………………………………..1分
所成的角(或其补角) ………………………………..1分
由已知,可得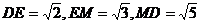 ,
,
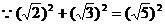
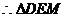 为直角三角形 …………………………………………………………….2分
为直角三角形 …………………………………………………………….2分
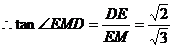 , …………………………………………………………….4分
, …………………………………………………………….4分
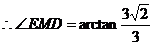 .
.
所以,异面直线OC与MD所成角的大小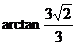 . …………………..1分
. …………………..1分
方法二(向量法)
以AB,AD,AO所在直线为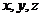 轴建立坐标系,
轴建立坐标系,
则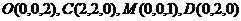 ,
………………………………………………2分
,
………………………………………………2分
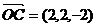 ,
,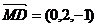 ,
…………………………………………………………………………..2分
,
…………………………………………………………………………..2分
设异面直线OC与MD所成角为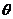 ,
,
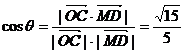 .……………………………………3分
.……………………………………3分
 OC与MD所成角的大小为
OC与MD所成角的大小为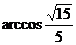 .……………………………………………1分
.……………………………………………1分
2007-2008年联考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com