
10.(2009浙江文)设等差数列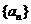 的前
的前 项和为
项和为 ,则
,则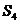 ,
,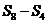 ,
,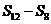 ,
,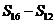 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列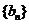 的前
的前 项积为
项积为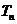 ,则
,则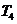 ,
, ,
,
, ,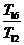 成等比数列.
成等比数列.
[命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力
答案: 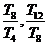
解析 对于等比数列,通过类比,有等比数列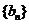 的前
的前 项积为
项积为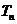 ,则
,则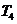 ,
,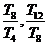 ,
,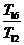 成等比数列.
成等比数列.
9.(2009浙江文)设等比数列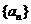 的公比
的公比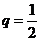 ,前
,前 项和为
项和为 ,则
,则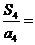 .
.
[命题意图]此题主要考查了数列中的等比数列的通项和求和公式,通过对数列知识点的考查充分体现了通项公式和前 项和的知识联系.
项和的知识联系.
答案 15
解析 对于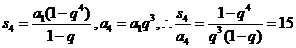


8.(2009四川卷文)等差数列{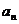 }的公差不为零,首项
}的公差不为零,首项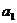 =1,
=1,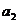 是
是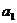 和
和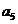 的等比中项,则数列的前10项之和是
的等比中项,则数列的前10项之和是
A. 90 B.
100
C. 145
D. 190 

[答案]B
[解析]设公差为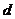 ,则
,则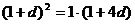 .∵
.∵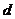 ≠0,解得
≠0,解得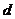 =2,∴
=2,∴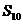 =10
=10
7.(2009江西卷理)数列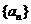 的通项
的通项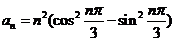 ,其前
,其前 项和为
项和为 ,则
,则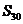 为
为
A.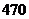 B.
B.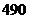 C.
C.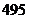 D.
D.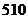
[答案] A
[解析]由于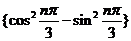 以3 为周期,故
以3 为周期,故
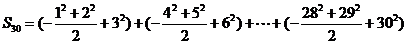
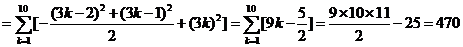 故选A
故选A
6..(2009安徽卷理)已知 为等差数列,
为等差数列,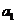 +
+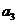 +
+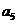 =105,
=105,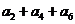 =99,以
=99,以 表示
表示 的前
的前 项和,则使得
项和,则使得 达到最大值的
达到最大值的 是
是
A.21 B.20 C.19 D. 18
[答案] B
[解析]由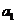 +
+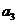 +
+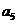 =105得
=105得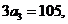 即
即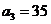 ,由
,由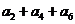 =99得
=99得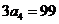 即
即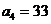 ,∴
,∴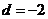 ,
,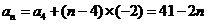 ,由
,由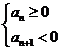 得
得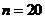 ,选B
,选B
5.(2009湖北卷文)古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如: 

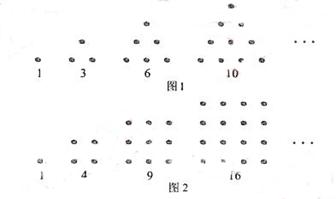


他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数。下列数中及时三角形数又是正方形数的是
A.289 B.1024 C.1225 D.1378
[答案]C
[解析]由图形可得三角形数构成的数列通项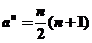 ,同理可得正方形数构成的数列通项
,同理可得正方形数构成的数列通项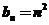 ,则由
,则由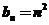
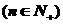 可排除A、D,又由
可排除A、D,又由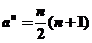 知
知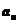 必为奇数,故选C.
必为奇数,故选C.
4.(2009湖北卷文)设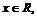 记不超过
记不超过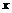 的最大整数为[
的最大整数为[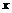 ],令{
],令{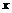 }=
}=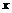 -[
-[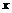 ],则
],则 {
{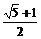 },[
},[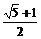 ],
],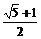
A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列
[答案]B
[解析]可分别求得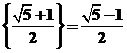 ,
,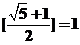 .则等比数列性质易得三者构成等比数列.
.则等比数列性质易得三者构成等比数列.
3.(2009宁夏海南卷理)等比数列 的前n项和为
的前n项和为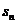 ,且4
,且4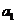 ,2
,2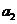 ,
,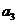 成等差数列。若
成等差数列。若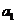 =1,则
=1,则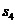 =( )
=( )
A.7 B.8 C.15 D.16
[解析]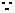 4
4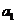 ,2
,2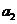 ,
,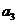 成等差数列,
成等差数列,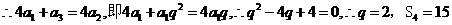 ,选C.
,选C.
[答案] C
2.(2009辽宁卷理)设等比数列{ 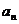 }的前n 项和为
}的前n 项和为 ,若
,若 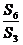 =3
,则
=3
,则 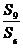 =
= 

A.
2 B. 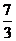 C.
C. 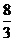 D.3
D.3
[解析]设公比为q ,则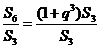 =1+q3=3 Þ q3=2
=1+q3=3 Þ q3=2
于是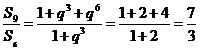


[答案]B
1.(2009广东卷理)已知等比数列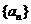 满足
满足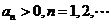 ,且
,且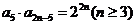 ,则当
,则当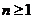 时,
时,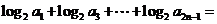


A.
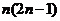 B.
B. 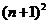 C.
C. 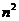 D.
D.
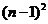
[解析]由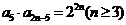 得
得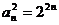 ,
,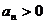 ,则
,则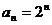 ,
,
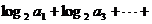
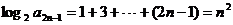 ,选C.
,选C. 

答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com