
1.(2009年广东卷文)已知等比数列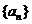 的公比为正数,且
的公比为正数,且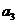 ·
·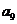 =2
=2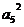 ,
,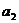 =1,则
=1,则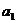 =
=
A. 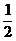 B.
B. 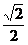 C.
C. 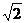 D.2
D.2
[答案]B
[解析]设公比为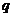 ,由已知得
,由已知得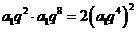 ,即
,即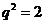 ,又因为等比数列
,又因为等比数列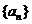 的公比为正数,所以
的公比为正数,所以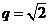 ,故
,故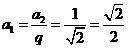 ,选B
,选B
2009年高考题
31.(本小题满分12分)(注意:在试题卷上作答无效)
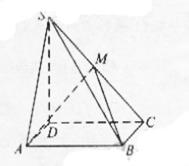 如图,四棱锥
如图,四棱锥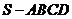 中,底面
中,底面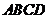 为矩形,
为矩形,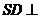 底面
底面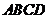 ,
, 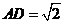
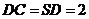 ,点M在侧棱
,点M在侧棱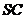 上,
上,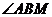 =60°
=60°
(I)证明:M在侧棱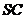 的中点
的中点
(II)求二面角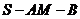 的大小。
的大小。
(I)解法一:作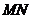 ∥
∥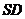 交
交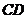 于N,作
于N,作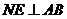 交
交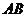 于E,
于E,
连ME、NB,则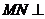 面
面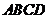 ,
,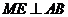 ,
,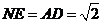
 设
设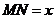 ,则
,则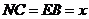 ,
,
在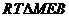 中,
中,
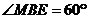
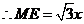 。
。
在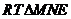 中由
中由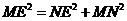
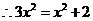
解得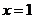 ,从而
,从而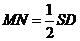
 M为侧棱
M为侧棱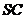 的中点M.
的中点M.
解法二:过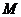 作
作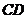 的平行线.
的平行线.
30.(本小题满分13分)
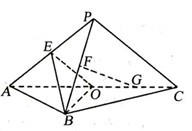
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,g和F式l上的两个不同点,且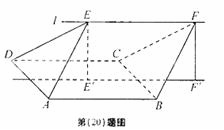 EA=ED,FB=FC,
EA=ED,FB=FC, 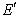 和
和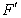 是平面ABCD内的两点,
是平面ABCD内的两点,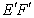 和
和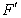
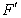 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线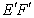 垂直且平分线段AD:
垂直且平分线段AD: 

(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面
体ABCDEF的体积。
[思路]根据空间线面关系可证线线垂直,由分割法可求得多面体体积,体现的是一种部分与整体的基本思想。
[解析](1)由于EA=ED且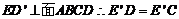
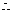 点E
点E 在线段AD的垂直平分线上,同理点F
在线段AD的垂直平分线上,同理点F 在线段BC的垂直平分线上.
在线段BC的垂直平分线上.
又ABCD是四方形
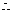 线段BC的垂直平分线也就是线段AD的垂直平分线
线段BC的垂直平分线也就是线段AD的垂直平分线
即点E F
F 都居线段AD的垂直平分线上.
都居线段AD的垂直平分线上. 

所以,直线E F
F 垂直平分线段AD.
垂直平分线段AD.
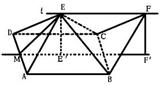 (2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分.设AD中点为M,在Rt△MEE
(2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分.设AD中点为M,在Rt△MEE 中,由于ME
中,由于ME =1,
=1,
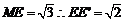 .
.
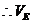 -ABCD
-ABCD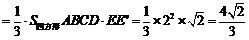
又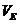 -BCF=VC-BEF=VC-BEA=VE-ABC
-BCF=VC-BEF=VC-BEA=VE-ABC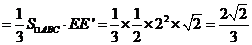
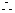 多面体ABCDEF的体积为VE-ABCD+VE-BCF=
多面体ABCDEF的体积为VE-ABCD+VE-BCF=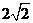
29.(本小题满分12分)
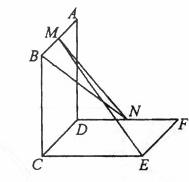
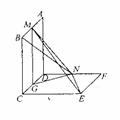
如图,已知两个正方行ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点 。
(I)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正值弦;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。 

 (I)解法一:
(I)解法一:
取CD的中点G,连接MG,NG。
设正方形ABCD,DCEF的边长为2,
则MG⊥CD,MG=2,NG=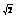 .
.
因为平面ABCD⊥平面DCED,
所以MG⊥平面DCEF,
可得∠MNG是MN与平面DCEF所成的角。因为MN=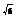 ,所以sin∠MNG=
,所以sin∠MNG=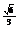 为MN与平面DCEF所成角的正弦值
……6分
为MN与平面DCEF所成角的正弦值
……6分
28.(Ⅰ)证明:连接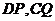 , 在
, 在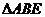 中,
中,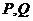 分别是
分别是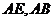 的中点,所以
的中点,所以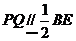 , 又
, 又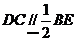 ,所以
,所以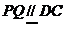 ,又
,又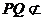 平面ACD ,DC
平面ACD ,DC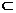 平面ACD,
所以
平面ACD,
所以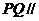 平面ACD
平面ACD
(Ⅱ)在 中,
中,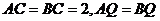 ,所以
,所以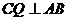
而DC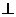 平面ABC,
平面ABC,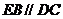 ,所以
,所以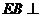 平面ABC
平面ABC
而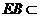 平面ABE,
所以平面ABE
平面ABE,
所以平面ABE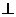 平面ABC,
所以
平面ABC,
所以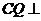 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以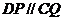
所以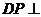 平面ABE,
所以直线AD在平面ABE内的射影是AP,
平面ABE,
所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是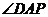
在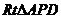 中,
中,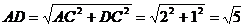 ,
,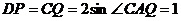
所以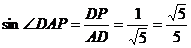
25. (本小题满分12分)
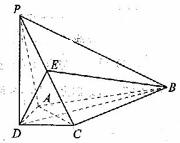 如图,在四棱锥
如图,在四棱锥 中,
中,
 平面
平面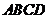 ,
,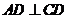 ,
,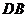 平分
平分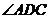 ,
,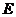 为的
为的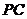 中点,
中点,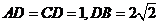
(1)证明: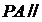 平面
平面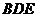


(2)证明: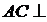 平面
平面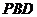
(3)求直线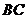 与平面
与平面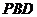 所成角的正切值
所成角的正切值
|
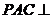 平面
平面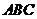 ,
,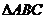
 是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,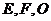 分别为
分别为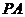 ,
,
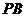 ,
, 的中点,
的中点,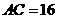 ,
,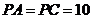 .
.
(I)设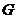 是
是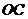 的中点,证明:
的中点,证明: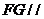 平面
平面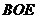 ;
;
(II)证明:在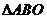 内存在一点
内存在一点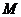 ,使
,使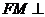 平面
平面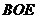 ,并求点
,并求点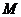 到
到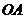 ,
,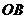 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为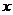 轴,
轴,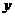 轴,
轴,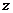 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O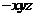 ,
,


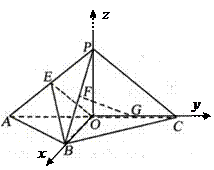 则
则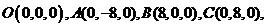
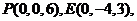
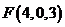 ,由题意得,
,由题意得,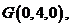 因
因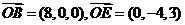 ,因此平面BOE的法向量为
,因此平面BOE的法向量为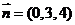 ,
,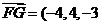 得
得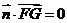 ,又直线
,又直线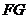 不在平面
不在平面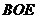 内,因此有
内,因此有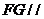 平面
平面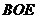
(II)设点M的坐标为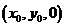 ,则
,则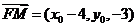 ,因为
,因为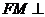 平面BOE,所以有
平面BOE,所以有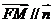 ,因此有
,因此有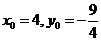 ,即点M的坐标为
,即点M的坐标为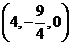 ,在平面直角坐标系
,在平面直角坐标系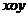 中,
中,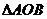 的内部区域满足不等式组
的内部区域满足不等式组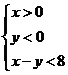 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在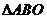 内存在一点
内存在一点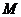 ,使
,使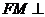 平面
平面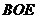 ,由点M的坐标得点
,由点M的坐标得点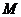 到
到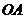 ,
,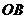 的距离为
的距离为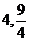 .
. 

|
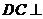 平面
平面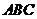 ,
,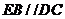 ,
,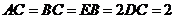 ,
,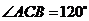 ,
,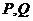 分别为
分别为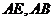 的中点.(I)证明:
的中点.(I)证明: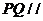 平面
平面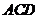 ;(II)求
;(II)求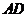 与平面
与平面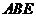 所成角的正弦值.
所成角的正弦值.24.(本小题满分12分)
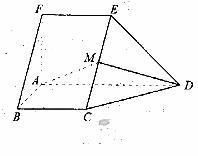 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 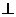 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB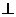 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=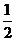 AD
AD 

(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD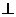 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。 

方法一:(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其
补角) 为异面直线BF与DE所成的角。设P为AD的中
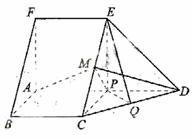 点,连结EP,PC。因为FE
点,连结EP,PC。因为FE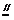 AP,所以FA
AP,所以FA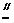 EP,同理AB
EP,同理AB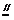 PC。
PC。
又FA⊥平面ABCD,所以EP⊥平面ABCD。而PC,AD
都在平面ABCD内,故EP⊥PC,EP⊥AD。由AB⊥AD,可
得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=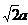 ,
,
故∠CED=60°。所以异面直线BF与DE所成的角的大小为60° 

(II)证明:因为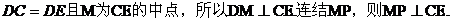
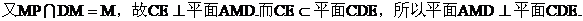 (III)
(III)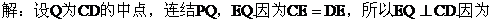
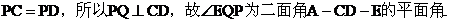
由(I)可得,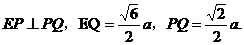
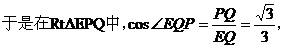


23.(本小题满分14分)
如图6,已知正方体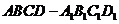 的棱长为2,点
的棱长为2,点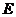 是正方形
是正方形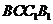 的中心,点
的中心,点
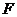 、
、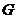 分别是棱
分别是棱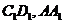 的中点.设点
的中点.设点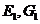 分别是点
分别是点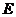 ,
,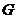 在平面
在平面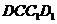 内的正投影.
内的正投影.
(1)求以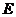 为顶点,以四边形
为顶点,以四边形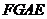 在平面
在平面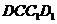 内的正投影为底面边界的棱锥的体积;
内的正投影为底面边界的棱锥的体积;
(2)证明:直线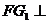 平面
平面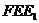 ;
;
(3)求异面直线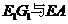 所成角的正弦值.
所成角的正弦值.
解:(1)依题作点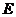 、
、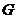 在平面
在平面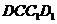 内的正投影
内的正投影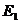 、
、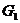 ,则
,则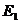 、
、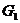 分别为
分别为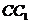 、
、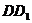 的中点,连结
的中点,连结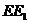 、
、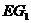 、
、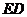 、
、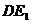 ,则所求为四棱锥
,则所求为四棱锥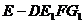 的体积,其底面
的体积,其底面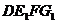 面积为
面积为
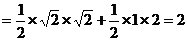 ,
,
又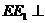 面
面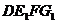 ,
,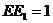 ,∴
,∴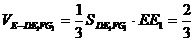 .
.
(2)以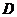 为坐标原点,
为坐标原点,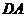 、
、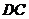 、
、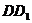 所在直线分别作
所在直线分别作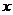 轴,
轴,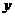 轴,
轴,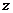 轴,得
轴,得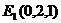 、
、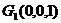 ,又
,又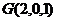 ,
,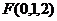 ,
,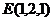 ,则
,则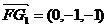 ,
,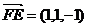 ,
,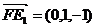 ,
,
∴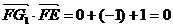 ,
,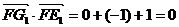 ,即
,即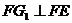 ,
,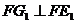 ,
,
又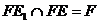 ,∴
,∴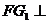 平面
平面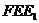 .
.
(3)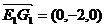 ,
,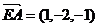 ,则
,则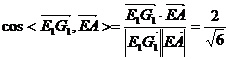 ,设异面直线
,设异面直线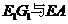 所成角为
所成角为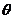 ,则
,则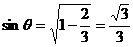 .
.
22. (本小题满分14分)
(本小题满分14分)
如图,在直三棱柱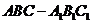 中,
中,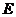 、
、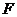 分别是
分别是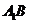 、
、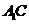 的中
的中
点,点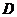 在
在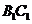 上,
上,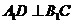 。
。
求证:(1)EF∥平面ABC; 
(2)平面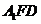
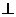 平面
平面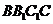 .
.
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查
空间想象能力、推理论证能力。满分14分。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com