
21.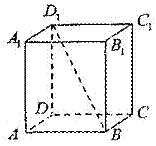 如图,若正四棱柱
如图,若正四棱柱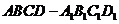 的底面连长为2,高 为
的底面连长为2,高 为
4,则异面直线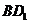 与AD所成角的大小是______________(结果
与AD所成角的大小是______________(结果
用反三角函数表示).
答案 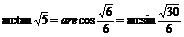
三、解答题
20.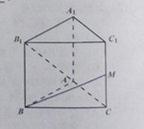 如图,已知正三棱柱
如图,已知正三棱柱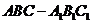 的各条棱长都相等,
的各条棱长都相等,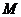 是侧
是侧
棱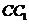 的中点,则异面直线
的中点,则异面直线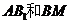 所成的角的大小
所成的角的大小
是 。
答案 

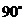
19. 已知二面角α-l-β为
已知二面角α-l-β为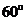 ,动点P、Q分别在面α、β内,P到β的距离为
,动点P、Q分别在面α、β内,P到β的距离为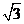 ,Q到α的距离为
,Q到α的距离为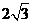 ,则P、Q两点之间距离的最小值为( C )
,则P、Q两点之间距离的最小值为( C )
(A) (B)2
(C)
(B)2
(C) 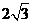 (D)4
(D)4 

解:如图分别作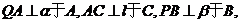
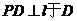 ,连
,连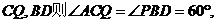
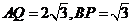 ,
,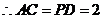
又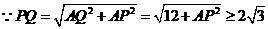
当且仅当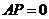 ,即
,即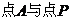 重合时取最小值。故答案选C。
重合时取最小值。故答案选C。 

18.已知三棱柱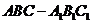 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,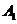 在底面
在底面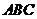 上的射影为
上的射影为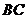 的
的
中点,则异面直线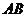 与
与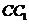 所成的角的余弦值为( D )
所成的角的余弦值为( D )
(A)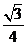 (B)
(B)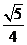 (C)
(C)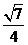 (D)
(D) 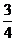


解:设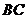 的中点为D,连结
的中点为D,连结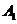 D,AD,易知
D,AD,易知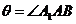 即为异面直线
即为异面直线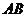 与
与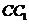 所 成的角,由三角余弦定理,易知
所 成的角,由三角余弦定理,易知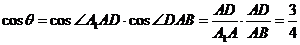 .故选D
.故选D 

17.对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。 

1相对棱AB与CD所在的直线异面;
2由顶点A作四面体的高,其垂足是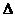 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作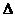 ABC和
ABC和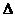 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
[解析]①④⑤
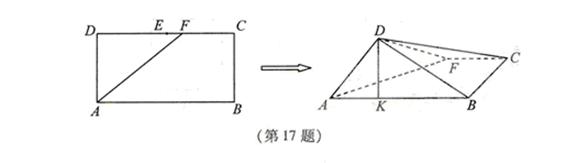
16.如图,在长方形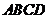 中,
中,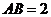 ,
,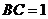 ,
,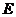 为
为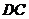 的中点,
的中点,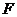 为线段
为线段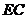 (端
(端
点除外)上一动点.现将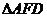 沿
沿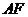 折起,使平面
折起,使平面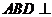 平面
平面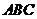 .在平面
.在平面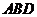 内过点
内过点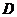 作
作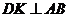 ,
,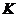 为垂足.设
为垂足.设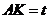 ,则
,则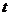 的取值范围是
.
的取值范围是
.
答案: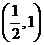
[解析]此题的破解可采用二个极端位置法,即对于F位于DC的中点时,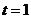 ,随着 F点到C点时,因
,随着 F点到C点时,因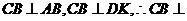 平面
平面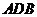 ,即有
,即有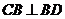 ,对于
,对于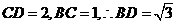 ,又
,又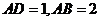 ,因此有
,因此有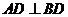 ,则有
,则有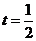 ,因此
,因此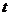 的取值范围是
的取值范围是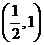


15.如图,已知六棱锥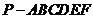 的底面是正六边形,
的底面是正六边形,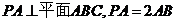 ,则
,则
下列结论正确的是
A.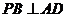 B.平面
B.平面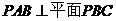


C. 直线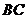 ∥平面
∥平面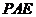 D.
D.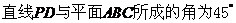
答案 D
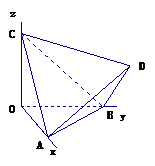
14.如图,正四面体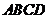 的顶点
的顶点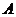 ,
,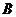 ,
,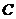 分别在两两垂直的三条射线
分别在两两垂直的三条射线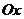 ,
,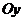 ,
, 上,则在下列命题中,错误的为
上,则在下列命题中,错误的为
 A.
A.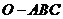 是正三棱锥
是正三棱锥
B.直线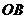 ∥平面
∥平面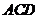
C.直线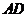 与
与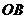 所成的角是
所成的角是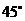
D.二面角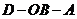 为
为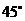


 答案 B
答案 B
13.平面六面体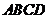 -
- 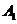
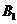
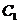
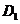 中,既与
中,既与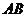 共面也与
共面也与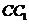 共面的棱的条数为[ C ]
共面的棱的条数为[ C ]
A.3 B. 4 C.5 D. 6


12.正方体ABCD-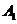
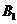
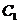
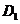 的棱上到异面直线AB,C
的棱上到异面直线AB,C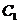 的
的
距离相等的点的个数为(C)
A.2
B.3 C.
4
D. 5 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com