
18. (本小题满分12分)(理科)从四名男生和三名女生中任选3人参加演讲比赛.
(Ⅰ)求所选3人中至少有一名女生的概率;
(Ⅱ)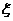 表示所选参加演讲比赛的人员中男生的人数,求
表示所选参加演讲比赛的人员中男生的人数,求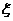 的分布列和数学期望.
的分布列和数学期望.
答案:(Ⅰ)记事件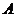 为“所选3人中至少有一名女生”,则其对立事件
为“所选3人中至少有一名女生”,则其对立事件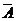 为“所选的3人全是男生”.
为“所选的3人全是男生”.
∴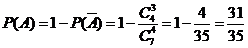 . ------------6分
. ------------6分
(Ⅱ)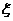 的可能取值为:
的可能取值为: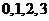 .
.
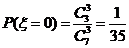 ,
,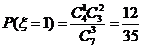 ,
,
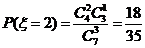 ,
,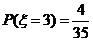 . ----------8分
. ----------8分
∴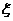 的分布列为:
的分布列为:
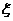 |
0 |
1 |
2 |
3 |
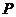 |
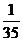 |
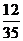 |
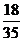 |
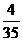 |
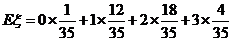 .
------------12分
.
------------12分
(文科)某班级有数学、自然科学、人文科学三个兴趣小组,各有三名成员,现从三个小组中各选出一人参加一个座谈会.
(I)求数学小组的甲同学没有被选中、自然小组的乙同学被选中的概率;
(II)求数学组的甲同学、自然小组的乙同学至少有一人不被选中的概率.
答案:我们把数学小组的三位成员记作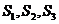 ,自然小组的三位成员记作
,自然小组的三位成员记作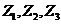 ,人文小组的三位成员记作
,人文小组的三位成员记作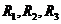 ,则基本事件是
,则基本事件是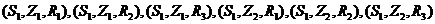 ,
,
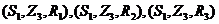 ,然后把这9个基本事件中
,然后把这9个基本事件中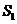 换成
换成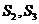 又各得
又各得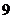 个基本事件,故基本事件的总数是
个基本事件,故基本事件的总数是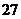 个.以
个.以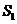 表示数学组中的甲同学、
表示数学组中的甲同学、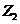 表示自然小组的乙同学.----------2分
表示自然小组的乙同学.----------2分
(I)甲同学没有选中、自然小组的乙同学被选中所含有的基本事件是上述基本事件中不含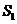 、含有
、含有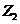 的基本事件,
的基本事件,
即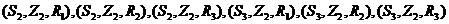 共6个基本事件,故所求的概率为
共6个基本事件,故所求的概率为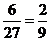 . ----------6分
. ----------6分
(II)“数学组的甲同学、自然小组的乙同学至少有一人不被选中”的对立事件是“数学组的甲同学、自然小组的乙同学都被选中”,这个事件所包含的基本事件是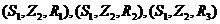 ,共3个基本事件,这个事件的概率是
,共3个基本事件,这个事件的概率是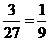 .
.
----------10分
根据对立事件的概率计算方法,所求的概率是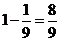 .----------12分
.----------12分
请把解答过程写在答题卡相应位置上.)
17. (本小题满分10分)已知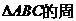 长为
长为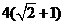 ,且
,且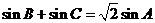 .
.
(I) 求边长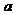 的值;
的值;
(II) 若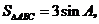 求
求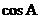 的值.
的值.
答案: (I)根据正弦定理,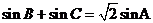 可化为
可化为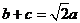 . ………2分
. ………2分
联立方程组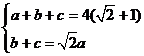 ,解得
,解得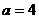 .
.
所以,边长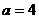 .
…………………………5分
.
…………………………5分
(II)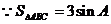 ,
,
∴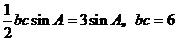 .
…………………………7分
.
…………………………7分
又由(I)可知,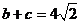 ,
,
∴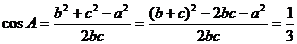 . …………………………10分
. …………………………10分
16. (理科)若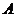 为不等式组
为不等式组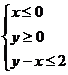 表示的平面区域,则当
表示的平面区域,则当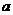 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线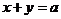 扫过
扫过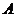 中的那部分区域的面积为 _____________.
中的那部分区域的面积为 _____________.
答案: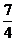
(文科)已知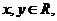 且满足不等式组
且满足不等式组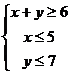 ,则
,则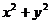 的最大值是
.
的最大值是
.
答案:74 注意到目标函数所表示的几何意义是动点到原点的距离的平方,作出可行域.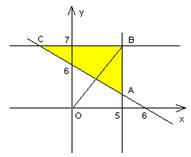 易知当为B点时取得目标函数的最大值可知B点的坐标为(5,7),
易知当为B点时取得目标函数的最大值可知B点的坐标为(5,7),
代入目标函数中,可得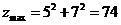 .
.
15. 长方体一顶点出发的三个侧面的面对角线的长分别为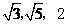 ,则该长方体外接球的表面积是______.
,则该长方体外接球的表面积是______.
答案: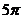 . 长方体一顶点出发的三条棱长的长分别为
. 长方体一顶点出发的三条棱长的长分别为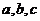 ,则
,则
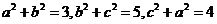 ,
,
得
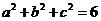 .
.
于是,球的直径2R满足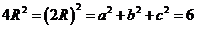 .
.
故外接球的表面积为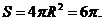
14. 在右面的数阵里,每行、每列的数依次均成等比数列, 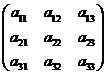
其中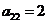 ,则所有数的乘积为_______.
,则所有数的乘积为_______.
答案:512. 利用等比中项公式,得
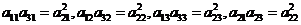 ,
,
于是,所有数的乘积为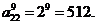
13. 在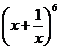 的展开式中,
的展开式中,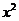 的系数为_______________(用数字作答).
的系数为_______________(用数字作答).
答案:15. 由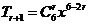 ,得
,得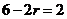 ,
,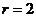 ,所以
,所以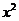 的系数为
的系数为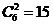 .
.
12. (理科)已知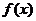 是定义在
是定义在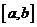 上的函数,其图像是一条连续的曲线,且满足下列条件:
上的函数,其图像是一条连续的曲线,且满足下列条件:
① 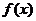 的值域为G,且
的值域为G,且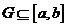 ;
;
② 对任意的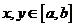 ,都有
,都有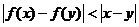 .
.
那么,关于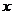 的方程
的方程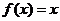 在区间
在区间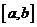 上根的情况是( )
上根的情况是( )
A.没有实数根 B. 有且仅有一个实数根
C. 恰有两个实数根 D. 有无数个不同的实数根
答案:B. 设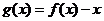 .
.
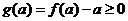 ,
,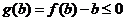 ,
所以
,
所以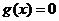 在
在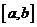 有实数根
若有两个不同的实数根
有实数根
若有两个不同的实数根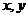 ,则
,则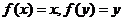 ,得
,得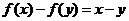 ,这与已知条件
,这与已知条件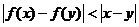 相矛盾. 故选B.
相矛盾. 故选B.
(文科)已知直线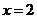 及
及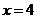 与函数
与函数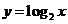 图像的交点分别为
图像的交点分别为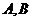 ,与函数
,与函数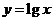 图像的交点分别为
图像的交点分别为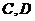 ,则直线AB与CD ( )
,则直线AB与CD ( )
A.相交,且交点在第I象限 B.相交,且交点在第II象限
C.相交,且交点在第IV象限 D.相交,且交点在坐标原点
答案:D.
第Ⅱ卷(非选择题,共90分)
11. 某单位需同时参加甲、乙、丙三个会议,甲需2人参加,乙、丙各需1人参加,从10人中选派4人参加这三个会议,不同的安排方法有( )
A.1260种 B.2025种 C.2520种 D.5040种
答案:C. 法一:从10人中选派4人有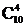 种,进而对选出的4人具体安排会议,有
种,进而对选出的4人具体安排会议,有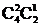 种,由分步计数原理得不同的选派方法为
种,由分步计数原理得不同的选派方法为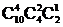 =2520种.
=2520种.
法二:据分步计数原理,不同选法种数为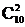 ·
·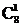 ·
·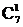 =2520种.
=2520种.
10.
将函数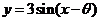 的图象
的图象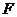 按向量
按向量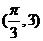 平移得到图象
平移得到图象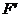 ,若
,若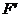 的一条对称轴是直线
的一条对称轴是直线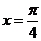 ,则
,则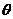 的一个可能取值是( )
的一个可能取值是( )
A 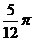 B
B
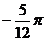 C
C
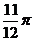 D
D
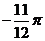
答案:A .由题意知平移后的解析式为: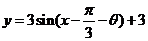 ,因它的对称轴是直线
,因它的对称轴是直线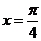 ,所以
,所以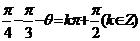 ,即
,即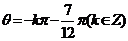 ,令
,令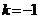 ,则
,则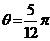 .
.
9. 已知二次曲线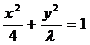 ,当离心率
,当离心率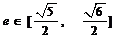 时,则实数
时,则实数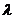 的取值范围是
的取值范围是
A.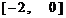 B.
B.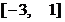
C.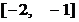 D.
D.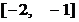
答案:C. 因为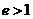 ,所以方程
,所以方程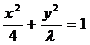 表示的曲线为双曲线,可以转化为
表示的曲线为双曲线,可以转化为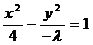 ,于是
,于是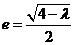 ,所以
,所以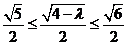 ,解得
,解得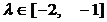 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com