2. 物块从斜面的底端以某一初速度沿粗糙斜面上滑至最高点后再沿斜面下滑至底端.下列说法正确的是：

A.上滑过程中摩擦力的冲量大于下滑过程中摩擦力的冲量　　

B.上滑过程中机械能损失等于下滑过程中机械能损失

C.上滑过程中物块的动量变化的方向与下滑过程中动量变化的方向相反

D.上滑过程中地面受到的压力大于下滑过程中地面受到的压力

1. 下列说法正确的是　　　　　　　　　　　　　

A．质点做自由落体运动，每秒内重力所做的功都相同

B．质点做平抛运动，每秒内动量的增量都相同

C．质点做匀速圆周运动，每秒内合外力的冲量都相同

D．质点做简谐运动，每四分之一周期内回复力做的功都相同

23．设数列{a_n}满足a₁＝a，a_n+1＝a_n²+a₁，．

(1)当a∈(－∞，－2)时，求证：M；

(2)当a∈(0，］时，求证：a∈M；

(3)当a∈(，+∞)时，判断元素a与集合M的关系，并证明你的结论．

22．一个暗箱中有形状和大小完全相同的3只白球与2只黑球，每次从中取出一只球，取到白球得2分，取到黑球得3分．甲从暗箱中有放回地依次取出3只球．

(1)写出甲总得分ξ的分布列；

(2)求甲总得分ξ的期望E(ξ)．

21．[选做题]在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．

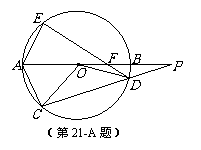A．选修4－1　几何证明选讲

如图，⊙O的直径AB的延长线与弦CD的延长线相交

于点P，E为⊙O上一点，AE=AC， DE交AB于点F．

求证：△PDF∽△POC．

B．选修4－2　矩阵与变换

若点A(2，2)在矩阵对应变换的作用下得到的点为B(－2，2)，求矩阵M的逆矩阵．

C．选修4－4　坐标系与参数方程

已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C₁：与曲线C₂：(t∈R)交于A、B两点．求证：OA⊥OB．

D．选修4－5　不等式选讲

已知x，y，z均为正数．求证：．

[必做题]第22题、第23题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．

23．已知数列{a_n}的前n项和为S_n，点(a_n+2，S_n+1)在直线y＝4x－5上，其中n∈N*，令b_n＝a_n+1－2a_n，且a₁＝1．

(1)求数列{b_n}的通项公式；

(2)若f(x)＝b₁x+b₂x²+b₃x³+…+b_nxⁿ，求f ¢(1)的表达式，并比较f ¢(1)与8n²－4n的大小．

22.某大楼共5层，4个人从第一层上电梯，假设每个人都等可能地在每一层下电梯，并且他们下电梯与否相互独立. 又知电梯只在有人下时才停止.

(I)求某乘客在第层下电梯的概率 ；

(Ⅱ)求电梯在第2层停下的概率；

(Ⅲ)求电梯停下的次数的数学期望.

(总分40分，加试时间30分钟)

答卷前，请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内．解答过程应写在答题卷的相应位置上，在其它地方答题无效。

21.B．选修4-2：矩阵与变换

已知矩阵M＝，N＝，求直线y＝2x+1在矩阵MN的作用下变换所得到的直线方程．

C．选修4-4：坐标系与参数方程

已知⊙C：r＝cosq+sinq，直线l：r＝．求⊙C上点到直线l距离的最小值．

20. 已知函数．

(Ⅰ)当时，求函数的单调区间；

(Ⅱ)若函数的图像在点处的切线的倾斜角为，问：m在什么范围取值时，对于任意的，函数在区间上总存在极值？

(Ⅲ)当时，设函数，若在区间上至少存在一个，使得成立，试求实数p的取值范围．

　　　　　　　　　　　　　　 高三数学试卷　 第4页 (共4页)

扬州市2010届高三第二次高考模拟考试样卷(二)

19. 各项均为正数的数列的前项和为，；

(1)求；

(2)令，，求的前项和．

(3)令(为常数，且)，，

是否存在实数对，使得数列成等比数列？若存在，求出实数对及数列