6．函数的定义域为一切实数，则实数m的取值范围是

A．[0，4)　　　 B．(0，4)　　 C．[4，+)　　　　　 D．[0，4][来源:学,科

5.已知＝2，关于p+q的取值范围的说法正确的是(　　 )

(A)一定不大于2　 　(B)一定不大于

(C)一定不小于　 　(D)一定不小于2

4．若复数,则|z|的值为(　 )

A．　　　　　 B．　　　　　　 C．　　　　 D．2

3．定义运算：，设函数，则函数是

A．奇函数　　 B．偶函数C．定义域内的单调函数　 D．周期函数

2．下列各组命题中，满足为真，为假，为真的是

A． ；

B．在中，若，则

　　　 在第一象限是增函数

C．

　　　 不等式的解集为

D．圆的面积被平分

　　　 ，

1.“因为指数函数是增函数(大前提)，而是指数函数(小前提)，所以 是增函数(结论)”，上面推理的错误是(　 )

A、大前提错导致结论错　　　　　　　 B、小前提错导致结论错　　　　

C、推理形式错导致结论错　　　　　　 D、大前提和小前提错都导致结论错

20.(本题满分16分)　

在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.

(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?

(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层，

(Ⅰ)共有几种不同的方案?

(Ⅱ)已知每根圆钢的直径为10cm，为考虑安全隐患，堆放高度不得高于4m，则选择哪个方案，最能节省堆放场地？

解：(1)当纵断面为正三角形时，设共堆放层,则从上到下每层圆钢根数是以1为首项、1为公差的等差数列，且剩余的圆钢一定小于根，从而由且得，当时，使剩余的圆钢尽可能地少，此时剩余了56根圆钢；………………6分

(2)(Ⅰ)当纵断面为等腰梯形时，设共堆放层,则从上到下每层圆钢根数是以为首项、1为公差的等差数列，从而，　　　　　　 ………………8分

即，因与的奇偶性不同，所以与的奇偶性也不同，且，从而由上述等式得：

或或或，所以共有4种方案可供选择.　　　　　　　　　　　　　　　　　　　　 ………………10分

(Ⅱ)因层数越多，最下层堆放得越少，占用面积也越少，所以由(2)可知：

若，则，说明最上层有29根圆钢，最下层有69根圆钢，此时如图所示，两腰之长为400 cm，上下底之长为280 cm和680cm，从而梯形之高为 cm，

而，所以符合条件；　　　　　　　　　　 ………………13分

若，则，说明最上层有17根圆钢，最下层有65根圆钢，此时如图所示，两腰之长为480 cm，上下底之长为160 cm和640cm，从而梯形之高为 cm，显然大于4m，不合条件，舍去；　　　　　　　　　　　　　　　　　　　　　　　　　　 ………………15分

综上所述，选择堆放41层这个方案，最能节省堆放场地.　　　　 ………………16分

19.(本题满分16分)　

已知是函数的一个极值点，其中，

(I)求与的关系式；

(II)求的单调区间；

(III)当时，函数的图象上任意一点的切线斜率恒大于3，求的取值范围.

解(I)因为是函数的一个极值点,所以,即，所以　　　　　 ……………………………………3分

(II)由(I)知，=……4分

当时，有，当变化时，与的变化如下表：

				1
	-	0	+	0	-
	单调递减	极小值	单调递增	极大值	单调递减

………………………………………………………………………………………………8分

故有上表知，当时，在单调递减，

在单调递增，在上单调递减.……………………………………………10分

(III)由已知得，即…………………………12分

又所以即①

设，其函数开口向上，由题意知①式恒成立，……13分

所以解之得又所以

即的取值范围为………………………………………………16分

18.(本题满分15分)

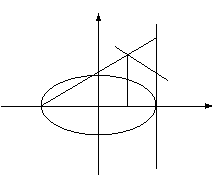如图，已知椭圆：的长轴长为4，离心率，为坐标原点，过的直线与轴垂直．是椭圆上异于、的任意一点，轴，为垂足，延长到点使得，连结延长交直线于点，为的中点．

(1)求椭圆的方程；

(2)证明点在以为直径的圆上；

(3)试判断直线与圆的位置关系．

解：(1)由题设可得，

解得，∴．∴椭圆的方程为．　　　 _{………………4分}

(2)设，则．

∵，∴．∴．∴点在以为圆心，2为半径的的圆上．即点在以为直径的圆上．　　　　　　　　　　　 _{………………9分}

(3)设，则，且．

又，∴直线的方程为．

令，得．又，为的中点，∴．

∴，．

∴

．∴．∴直线与圆相切．_{………………15分}

_{(用其他方法证明的同学按标准给分)}

17．(本题满分15分)

　已知等差数列中，.

　(1)求的通项公式；

　(2)调整数列的前三项的顺序，使它成为等比数列的前三项，求的前项和.

解：(1)由已知，得求得，　　　　　　　　 _{………………………4分}

　　 ∴的公差d=3　　　　　　　　　　　　　　 　　_{………………………5分}

∴a_n=a₁+(n－1)d=－2+3(n－1)=3n－5.　　　　　　　　　　　 _{………………7分}

　 (2)由(1)，得a₃=a₂+d=1+3=4，∴a₁=－2，a₂=1，a₃=4.

　　　　 依题意可得：数列{b_n}的前三项为

b₁=1，b₂=－2，b₃=4或b₁==4，b₂=－2，b₃=1　　　 _{………………9分}

　 (i)当数列{b_n}的前三项为b₁=1，b₂=－2，b₃=4时，则q=－2 .

　　　　 .　　　　　 _{………………12分}

　 (ii)当数列{b_n}的前三项为b₁=4，b₂=－2，b₃=1时，则

　　　　 . 　_{………………15分}