7．已知表示三条不同的直线，表示三个不同平面，有下列四个命题：

①若，且，则；

②若相交且都在外，，，，，则；

③若，，，，则；

④若则.其中正确的是▲

6．设，则不等式

()成立的充要条件是　　▲　　.(注：填写的取值范围)u.

5．运行右边算法流程，当输入的值为　　 ▲　　 时，

输出的值为4．

　　　　　　　　　　　　　 高三数学试卷 第1页 (共4页)

4．若，其中是虚数单位，则　 ▲　 ．

3．若函数在上是减函数，

则 　　▲　　

2．若函数是偶函数，且在

上是减函数，则　 ▲　

1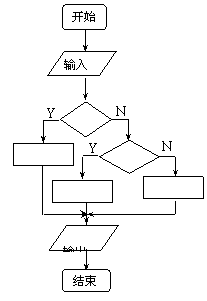．已知全集，集合，

则　 　▲ 　　　

第 一 部 分

20．[解](1)对于非零常数T，f(x+T)=x+T, Tf(x)=Tx. 因为对任意x∈R，x+T= Tx不能恒成立，所以f(x)=　　　　　　　　　　　　　 ………………3分　　　

(2)因为函数f(x)=a^x(a>0且a≠1)的图象与函数y=x的图象有公共点，

所以方程组：有解，消去y得a^x=x,显然x=0不是方程a^x=x的解，所以存在非零常数T，使a^T=T.　　 　于是对于f(x)=a^x有 故f(x)=a^x∈M.　　　　　　　　　　　　　　　　　　　　　 ………………8分

(3)当k=0时，f(x)=0，显然f(x)=0∈M.

当k≠0时，因为f(x)=sinkx∈M，所以存在非零常数T，对任意x∈R，有

f(x+T)=T f(x)成立，即sin(kx+kT)=Tsinkx .

因为k≠0，且x∈R，所以kx∈R，kx+kT∈R，

于是sinkx ∈[－1，1]，sin(kx+kT) ∈[－1，1]，

故要使sin(kx+kT)=Tsinkx .成立，

只有T=，当T=1时，sin(kx+k)=sinkx 成立，则k=2mπ, m∈Z .

当T=－1时，sin(kx－k)=－sinkx 成立，

即sin(kx－k+π)= sinkx 成立，

则－k+π=2mπ, m∈Z ，即k=－2(m－1) π, m∈Z .

综合得，实数k的取值范围是{k|k= mπ, m∈Z}　　　 ………………16分

19.解：(1)设从A地运出的油量为a，根据题设，直接运油到B地，往返油耗等于a，

所以B地收到的油量为(1－)a．所以运油率P₁＝＝．………… …3分

而从A地运出的油量为a时，C地收到的油量为(1－)a，

B地收到的油量(1－)(1－)a，所以运油率P₂＝

＝(1－)(1－)＝(+)(1－)．…………………………7分

所以P₂－P₁＝x(1－x)，因为0＜x＜1，所以P₂－P₁＞0，即P₂＞P₁． …………10分

(2)因为P₂＝(+)(1－)≤＝．

当且仅当+＝1－，即x＝时，取“＝”．

所以当C地为AB中点时，运油率P₂有最大值．……………………………16分