12．解：(I) ,由得，或

而，列出下表

		0
	-	0	+	0	-
	递减	极小值	递增	极大值	递减

所以，当时，取得极小值，极小值等于；

当时，取得极大值，极大值等于；

(II)设函数、，　　 不妨设

(注：若直接用来证明至少扣1分)

(III)时，

10．(1)[证明]∵△PAB中， D为AB中点，M为PB中点，∴

∵DM平面，PA平面，∴平面　　　　　　

(2)[证明]∵D是AB的中点，△PDB是正三角形，AB=20，

∴ ∴△PAB是直角三角形，且AP⊥PB，

又∵AP⊥PC，∴AP⊥平面PBC．∴AP⊥BC．

又∵AC⊥BC， AP∩AC=A，∴BC⊥平面PAC．∵ ∴平面PAC⊥平面ABC．

(3)[解]由(1)知，由(2)知PA⊥平面PBC，　 ∴DM⊥平面PBC．

∵正三角形PDB中易求得，

∴

11．(Ⅰ)由题设知

由于，则有，所以点的坐标为

故所在直线方程为,所以坐标原点到直线的距离为

又，所以　 解得： ,所求椭圆的方程为

(Ⅱ)由题意可知直线的斜率存在，设直线斜率为

直线的方程为，则有

设，由于、、三点共线，且

根据题意得,解得或

又在椭圆上，故或

解得,综上，直线的斜率为或.

6.　 7.　 8.　　 9.　

1.　 2. 　　　3.4　　 4. 　　5.　

12．已知函数．(I)当时，求函数的极值；(II) 若函数的图象上任意不同的两点连线的斜率都小于2，求证：；(III)对任意的图像在处的切线的斜率为，求证：是成立的充要条件．

江苏省泰州中学2010届高三数学基础题训练

(20)答案

11．设椭圆的左右焦点分别为、，是椭圆上的一点，且，坐标原点到直线的距离为．

(Ⅰ)求椭圆的方程；(Ⅱ)设是椭圆上的一点，过点的直线交轴于点，交轴于点，若，求直线的斜率．

10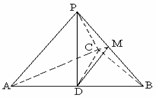．如图，已知三棱锥P-ABC，∠ACB=90°，CB=4，AB=20，D为AB中点，M为PB的中点，且△PDB是正三角形，PA⊥PC．(I)求证：平面；(II)求证：平面PAC⊥平面ABC；

(Ⅲ)若M为PB的中点，求三棱锥M-BCD的体积．

9、设函数，若用[]表示不超过实数的最大整数，则函数[][]的值域为______________.

8．如图，一个类似杨辉三角的递推式，则(1)第n行

的首尾两数均为　　　　 ，(2)第n行的第2个数为　　　　 .

7.若曲线x²+y²-4x-4y-10=0上至少有三个不同的点到直线l:ax+by=0的距离为2,则直线l的斜率的取值范围是　 　　　　　　　.