
2、(本小题满分14分)
已知函数 ,
, .
.
(I)求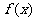 的最大值和最小值;
的最大值和最小值;
(II)若不等式 在
在 上恒成立,求实数
上恒成立,求实数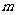 的取值范围.
的取值范围.
1. (本小题满分10分)
已知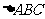 中,
中,  、
、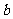 、
、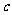 分别是角A、B、C的对边,A是锐角。且
分别是角A、B、C的对边,A是锐角。且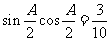 ,
,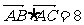
(Ⅰ)求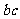 的值;
的值;
(Ⅱ)求 的最小值.
的最小值.
3. (本题满分12分)
某大学经济学院上学期开设了《概率论与数理统计》,该学院共有2000名学生修习了这门课程,且学生的考试成绩全部合格(答卷存档),其中优秀、良好、合格三个等级的男、女学生人数如下表,但优秀等级的男、女学生人数缺失,分别用x、y代替.
|
|
优秀 |
良好 |
合格 |
|
男生人数 |
x |
370 |
377 |
|
女生人数 |
y |
380 |
373 |
(1)若用分层抽样法在所有2000份学生答卷中随机抽取60份答卷进行比较分析,求在优秀等级的学生中应抽取多少份答卷?
(2)若x≥245,y≥245,求优秀等级的学生中女生人数比男生人数多的概率.
2.四棱锥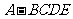 中,底面
中,底面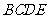 为矩形,
为矩形,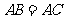 ,
,
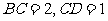 .并且侧面
.并且侧面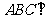 底面
底面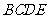 ,
,
(Ⅰ)取 的中点为
的中点为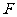 ,
, 的中点为
的中点为 ,证明:
,证明: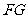 ∥面
∥面 ;
;
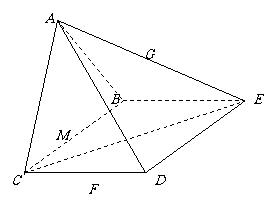 (Ⅱ)若
(Ⅱ)若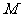 为
为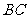 中点,求证:
中点,求证: .
.

1.已知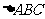 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为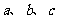 ,向量
,向量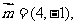
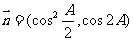 ,且
,且 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若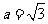 ,bc=3,试判断
,bc=3,试判断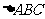 形状.
形状.
3. (12分)如图,在三棱柱
(12分)如图,在三棱柱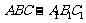 中,
中, ,
,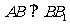 ,
, ,
,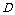 为
为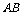 的中点,且
的中点,且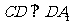 .
.
⑴求证: 平面
平面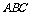 ;
;
⑵求证: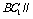 平面
平面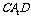 ;
;
⑶求三棱锥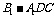 的体积.
的体积.
2.(本小题共12分)
某商场举行抽奖活动,从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中三等奖的概率;(2)求中奖的概率。
1.(本小题共12分)
已知向量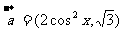 ,
,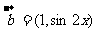 ,函数
,函数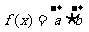 ,
, .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)在
 中,
中,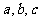 分别是角
分别是角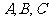 的对边,且
的对边,且 ,
,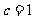 ,
,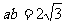 ,且
,且 ,求
,求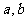 的值.
的值.
3.已知函数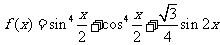 .
.
(Ⅰ)求函数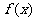 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)若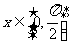 ,求
,求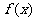 的最值,并求出取最值时
的最值,并求出取最值时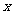 的值.
的值.
2、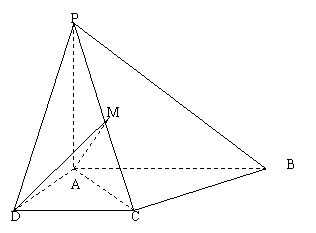 (14分)如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB‖CD,
(14分)如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB‖CD, ABC=45°,DC=1,AB=2,PA
ABC=45°,DC=1,AB=2,PA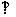 平面ABCD,PA=1
平面ABCD,PA=1
(1)求证:AB‖平面PCD
(2)求证:BC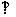 平面PAC
平面PAC
(3)若M是PC的中点,求三棱锥M-ACD的体积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com